Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB // CD) cắt nhau tại điểm E trên cạnh đáy CD

Bài 3.7 trang 55 Toán 8 Tập 1: Hai tia phân giác của hai góc A, B của hình thang cân ABCD (AB // CD) cắt nhau tại điểm E trên cạnh đáy CD. Chứng minh rằng EC = ED.

Trả lời

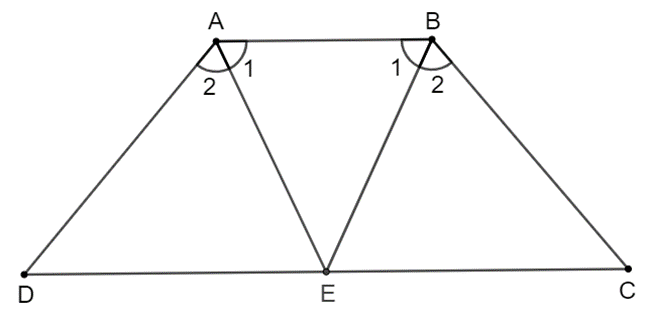
Vì ABCD là hình thang cân nên $\widehat{DAB}=\widehat{ABC};\hat{C}=\hat{D};AD=BC$ .

Theo đề bài, ta có AE, BE lần lượt là tia phân giác của $\widehat{BAD}$ và $\widehat{ABC}$ .

Suy ra ${\hat{A}}_1={\hat{A}}_2=\frac{1}{2}\widehat{DAB};{\hat{B}}_1={\hat{B}}_2=\frac{1}{2}\widehat{ABC}$ .

Mà $\widehat{DAB}=\widehat{ABC}$ nên ${\hat{A}}_1={\hat{A}}_2={\hat{B}}_1={\hat{B}}_2$ .

Xét tam giác EAB cân tại E (vì ${\hat{A}}_1={\hat{B}}_1$ ) nên EA = EB.

Xét ∆ADE và ∆BCE có:

EA = EB (chứng minh trên);

${\hat{A}}_2={\hat{B}}_2$ (chứng minh trên);

AD = BC (chứng minh trên)

Do đó ∆ADE = ∆BCE (c.g.c).

Suy ra EC = ED (hai cạnh tương ứng).

Xem thêm các bài giải SGK Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 2