Cho hình thang cân ABCD, AB // CD và AB < CD (H.3.16). a) Từ A và B kẻ AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD

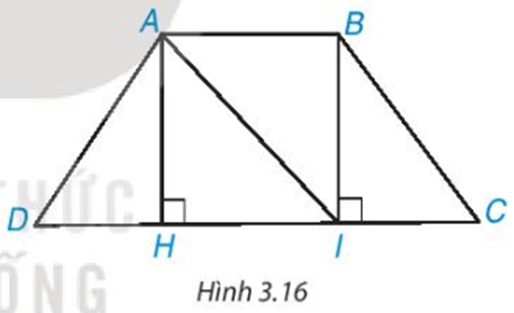
HĐ1 trang 53 Toán 8 Tập 1: Cho hình thang cân ABCD, AB // CD và AB < CD (H.3.16).

a) Từ A và B kẻ AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD. Chứng minh rằng AH = BI bằng cách chứng minh ∆AHI = ∆IBA.

b) Chứng minh ∆AHD = ∆BIC, từ đó suy ra AD = BC.

Trả lời

a) Vì ABCD là hình thang cân (AB // CD) nên $\widehat{BAI}=\widehat{AIH}$ (hai góc so le trong).

Ta có AH ⊥ DC, BI ⊥ DC suy ra AH // BI.

Do đó $\widehat{AIB}=\widehat{HAI}$ (hai góc so le trong).

Xét ∆AHI và ∆IBA có:

$\widehat{BAI}=\widehat{AIH}$ (chứng minh trên);

Cạnh AI chung;

$\widehat{AIB}=\widehat{HAI}$ (hai góc so le trong).

Do đó ∆AHI = ∆IBA (c.g.c).

Suy ra AH = BI (hai cạnh tương ứng).

b) Vì ABCD là hình thang cân (AB // CD) nên $\hat{C}=\hat{D}$ (1)

Xét ∆AHD vuông tại H có $\widehat{DAH}+\hat{D}=90°$ (2) (trong tam giác vuông, hai góc nhọn có tổng số đo bằng 90°).

Tương tự, ∆BIC vuông tại I có $\widehat{CBI}+\hat{C}=90°$ (3)

Từ (1), (2) và (3) suy ra $\widehat{DAH}=\widehat{CBI}$ .

Xét ∆AHD và ∆BIC có:

$\widehat{AHD}=\widehat{BIC}=90°$ (vì AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD);

AH = BI (chứng minh câu a);

$\widehat{DAH}=\widehat{CBI}$ (chứng minh trên).

Do đó ∆AHD = ∆BIC (cạnh góc vuông – góc nhọn kề).

Suy ra AD = BC (hai cạnh tương ứng).

Xem thêm các bài giải SGK Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 2