Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BD tại D

Bài 3.5 trang 55 Toán 8 Tập 1: Cho hình thang ABCD (AB // CD). Kẻ đường thẳng vuông góc với AC tại C và đường thẳng vuông góc với BD tại D, hai đường thẳng này cắt nhau tại E. Chứng minh rằng nếu EC = ED thì hình thang ABCD là hình thang cân.

Trả lời

Gọi O là giao điểm của AC và BD.

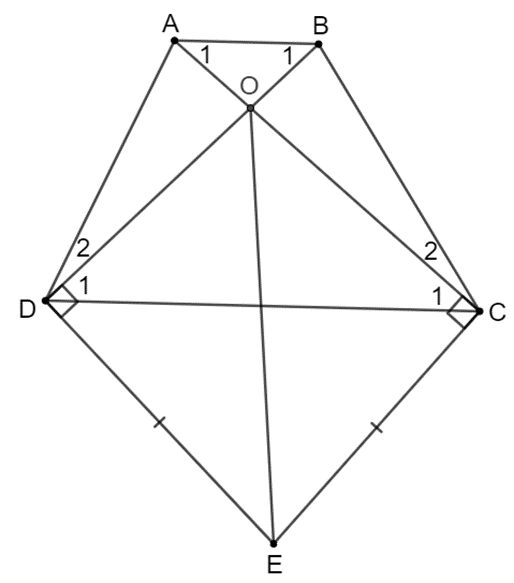
Xét ∆DOE và ∆COE có:

$\widehat{ODE}=\widehat{OCE}=90°$ (vì OD ⊥ DE; OC ⊥ CE);

EC = ED (giả thiết);

Cạnh OE chung

Do đó ∆DOE = ∆COE (cạnh huyền – cạnh góc vuông).

Suy ra OC = OD (hai cạnh tương ứng) (1)

Do đó tam giác OCD cân tại O nên ${\hat{C}}_1={\hat{D}}_1$ .

Vì ABCD là hình thang nên AB // CD suy ra ${\hat{A}}_1={\hat{C}}_1;{\hat{B}}_1={\hat{D}}_1$ (cặp góc so le trong).

Do đó ${\hat{A}}_1={\hat{B}}_1$ (vì ${\hat{C}}_1={\hat{D}}_1$ ).

Suy ra tam giác OAB cân tại O nên OA = OB (2)

Ta có: AC = OA + OC và BD = OB + OD (3)

Từ (1), (2) và (3) suy ra AC = BD

Hình thang ABCD có AC = BD nên ABCD là hình thang cân.

Xem thêm các bài giải SGK Toán 8 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 2