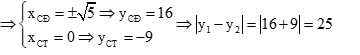Gọi y1, y2 lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số y = -x^4 + 10x^2 - 9. Khi đó
38
28/04/2024
Gọi \({y_1},\,{y_2}\) lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số \(y = - {x^4} + 10{x^2} - 9\) . Khi đó, \(\left| {{y_1} - {y_2}} \right|\) bằng:
A. 7
B. \(2\sqrt 5 \)
C. 25
Trả lời
Đáp án C
Phương pháp:
+) Giải phương trình\(y' = 0\) tìm các điểm cực trị của hàm số.
+) Tính các giá trị cực trị của hàm số.
Cách giải:
\(y = {x^4} + 10{x^2} - 9 \Rightarrow y' = - 4{x^3} + 20x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 5 \end{array} \right.\)
Bảng xét dấu y’: