Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số đồng biến trên khoảng . Số phần tử của S là A. 10 B. 7 C. 9. D. 8
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số 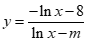 đồng biến trên khoảng
đồng biến trên khoảng 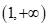 . Số phần tử của S là
. Số phần tử của S là
A. 10.
B. 7.
C. 9.
D. 8.
