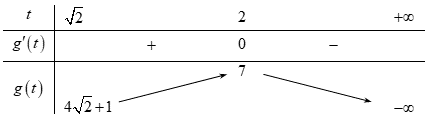
Gọi M là giá trị lớn nhất của hàm số y = f( x ) = 4 căn bậc hai của x^2- 2x + 3 + 2x - x^2. Tính tích các nghiệm của phương trình f( x ) = M A. 2 B. 0 C. - 1. D. 1
47
03/05/2024
Gọi \(M\)là giá trị lớn nhất của hàm số \(y = f\left( x \right) = 4\sqrt {{x^2} - 2x + 3} + 2x - {x^2}\). Tính tích các nghiệm của phương trình \(f\left( x \right) = M\).
A. \(2\).
B. \(0\).
C. \( - 1\).
D. \(1\).
Trả lời
Lời giải
Chọn C
Tập xác định của hàm số: \(D = \mathbb{R}\).
Đặt \(t = \sqrt {{x^2} - 2x + 3} = \sqrt {{{\left( {x - 1} \right)}^2} + 2} \ge \sqrt 2 \)Ta có \(g\left( t \right) = 4t + 3 - {t^2}\)với \(t \in \left[ {\sqrt 2 ; + \infty } \right)\).
Có \(g'\left( t \right) = 4 - 2t\); \(g'\left( t \right) = 0\)\( \Leftrightarrow t = 2\).
Bảng biến thiên:
Vậy \(\mathop {\max }\limits_{\left[ {\sqrt 2 ; + \infty } \right)} {\mkern 1mu} g\left( t \right) = \max f\left( x \right) = 7\)khi \(t = 2\)hay \({x^2} - 2x - 1 = 0\)nên tích hai nghiệm bằng \( - 1\).
