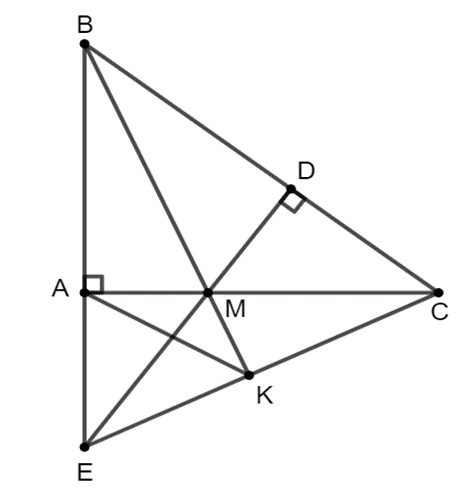
Gọi E là giao điểm của đường thẳng AB với đường thẳng MD. Chứng minh rằng DB . DC = DE . DM
Cho tam giác ABC vuông tại A (AB < AC), M là điểm bất kì trên cạnh AC. Kẻ MD ⊥ BC (D ∈ BC).
Gọi E là giao điểm của đường thẳng AB với đường thẳng MD.
Chứng minh rằng DB . DC = DE . DM.