Đường thẳng BM cắt EC tại K. Chứng minh rằng \[\widehat {EKA} = \widehat {EBC}\].

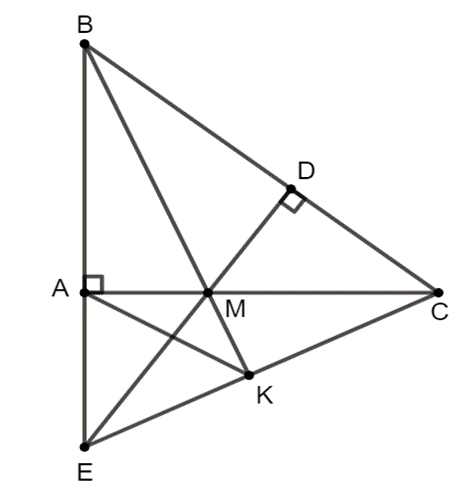
Xét ∆BEC có đường cao CA và BE cắt nhau tại M, suy ra M là trực tâm ∆BEC.

Do đó BK ⊥ EC.

Xét ∆EAC vuông tại A và ∆EKB vuông tại K có \[\widehat {BEC}\] chung.

Do đó ∆EAC ᔕ ∆EKB (g.g)

Suy ra \[\frac{{EA}}{{EK}} = \frac{{EC}}{{EB}}\] hay \[\frac{{EA}}{{EC}} = \frac{{EK}}{{EB}}\].

Xét ∆EAK và ∆ECB có \[\frac{{EA}}{{EC}} = \frac{{EK}}{{EB}}\] và \[\widehat {BEC}\] chung.

Do đó ∆EAK ᔕ ∆ECB (c.g.c).

Suy ra \[\widehat {EKA} = \widehat {EBC}\] (các góc tương ứng).