Đồ thị hàm số y = x^3 - 3x^2 - 2 và đường thẳng y = 2 có bao nhiêu điểm chung? A. 0. B. 1 C. 3 D. 2
Đồ thị hàm số \(y = {x^3} - 3{x^2} - 2\) và đường thẳng \(y = 2\) có bao nhiêu điểm chung?
A. 0.
B. \(1\).
C. \(3\).
D. \(2\).
Lời giải
Chọn B
Ta có \(y = {x^3} - 3{x^2} - 2\backslash \left( {\;\backslash Rightarrow\;\backslash } \right)\)\(y' = 3{x^2} - 6x\); \(y' = 0\backslash \left( {\;\backslash Leftrightarrow\;\backslash } \right)\)\(\left[ {\begin{array}{*{20}{c}}{x = 0 \Rightarrow y = - 2}\\{x = 2 \Rightarrow y = - 6}\end{array}} \right.\).
Bảng biến thiên hàm số \(y = {x^3} - 3{x^2} - 2\):
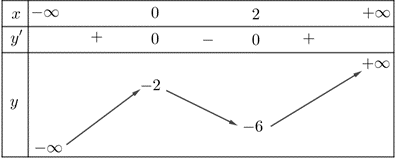
Dựa vào bảng biến thiên ta thấy đường thẳng \(y = 2\) và đồ thị hàm số \(y = {x^3} - 3{x^2} - 2\) có \(1\) điểm chung duy nhất.