Diện tích S của mặt cầu ngoại tiếp hình lập phương ABCD.A’B’C’D’ cạnh a là

D. $3\pi {a^2}$

Đáp án D

Phương pháp:

Diện tích mặt cầu có bán kính R là: $S = 4\pi {R^2}$

Cách giải:

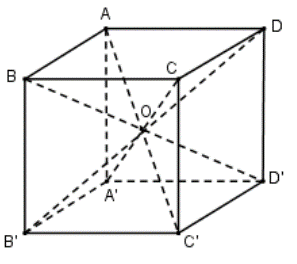
Hình lập phương ABCD.A’B’C’D’ có bán kính mặt cầu ngoại tiếp

$R = \frac{1}{2}AC' = \frac{1}{2}\sqrt {A{C^2} + AA{'^2}} = \frac{1}{2}\sqrt {A{B^2} + A{D^2} + AA{'^2}} = \frac{1}{2}a\sqrt 3$

Diện tích mặt cầu đó là: $S = 4\pi {R^2} = 4\pi .{\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = 3\pi {a^2}$