Lời giải

Chọn D

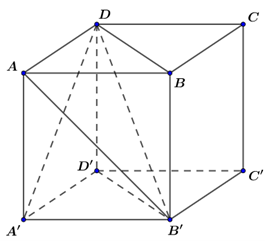
+ Chia khối lập phương \(ABCD.A'B'C'D'\) thành hai khối lăng trụ bằng nhau \(ABD.A'B'D'\) và \(BCD.B'C'D'\)

+ Xét khối lăng trụ \(ABD.A'B'D'\)và nối các đường như hình vẽ trên.

-Ta thấy hai khối tứ diện \(D'A'B'D\) và \(AA'B'D\) bằng nhau vì chúng đối xứng với nhau qua mặt phẳng \(\left( {A'B'D} \right)\).

-Hai khối tứ diện \(BAB'D\) và \(A'AB'D\) bằng nhau vì chúng đối xứng với nhau qua mặt phẳng \(\left( {AB'D} \right)\).Như vậy khối lăng trụ \(ABD.A'B'D'\)được chia thành 3 khối tứ diện \(D'A'B'D\),\(AA'B'D\) và \(BAB'D\)bằng nhau.

+ Làm tương tự như vậy với khối lăng trụ \(BCD.B'C'D'\)ta cũng chia được 3 khối tứ diện bằng nhau.

+ Vậy ta có thể chia khối lập phương thành 6 khối tứ diện bằng nhau.