Có hai xã cùng ở một bên bờ sông Lam. Các kĩ sư muốn bắc một cây cầu qua sông Lam cho người dân hai xã
411
15/11/2023
Bài 3 trang 86, trang 87 Toán 7 Tập 2: Có hai xã cùng ở một bên bờ sông Lam. Các kĩ sư muốn bắc một cây cầu qua sông Lam cho người dân hai xã. Để thuận lợi cho người dân đi lại, các kĩ sư cần phải chọn vị trí của cây cầu sao cho tổng khoảng cách từ hai xã đến chân cầu là nhỏ nhất. Bạn Nam đề xuất cách xác định vị trí của cây cầu như sau (Hình 54):
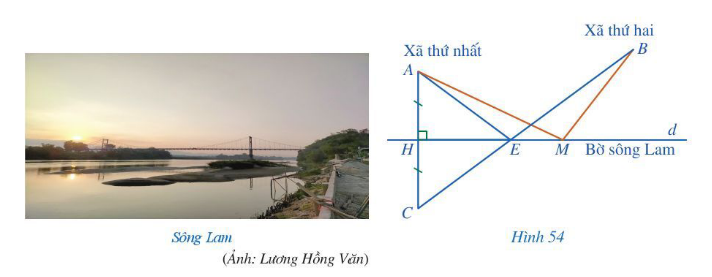
– Kí hiệu điểm A chỉ vị trí xã thứ nhất, điểm B chỉ vị trí xã thứ hai, đường thẳng d chỉ vị trí bờ sông Lam.
– Kẻ AH vuông góc với d (H thuộc d), kéo dài AH về phía H và lấy điểm C sao cho AH = HC.
– Nối C với B, CB cắt đường thẳng d tại điểm E.
Khi đó, E là vị trí của cây cầu.
Bạn Nam nói rằng: Lấy một điểm M trên đường thẳng d, M khác E thì
MA + MB > EA + EB.
Em hãy cho biết bạn Nam nói đúng hay sai. Vì sao?
Trả lời
Vị trí của hai xã và bờ sông Lam được mô tả như hình vẽ.
|
GT
|
Đường thẳng d,
A, B nằm cùng một phía với d
AH⊥d (H ∈ d), AH = HC
BC cắt d tại E, M ∈ d
|
|
KL
|
Khẳng định MA + MB > EA + EB là đúng hay sai? Vì sao?
|
Chứng minh (Hình dưới đây):
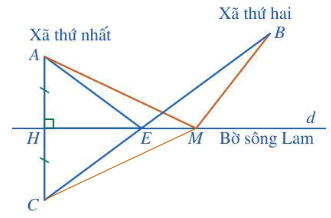
Nối đoạn thẳng CM.
+) Vì AH⊥d (H ∈ d) nên ^AHE=^CHE=90°
Do đó tam giác AHE (vuông tại H) và tam giác CHE (vuông tại H).
Xét tam giác AHE (vuông tại H) và tam giác CHE (vuông tại H) ta có:
AH = CH (giả thiết)
HE là cạnh chung
Suy ra ∆AHE = ∆CHE (hai cạnh góc vuông)
Do đó AE = CE (hai cạnh tương ứng)
Nên EA + EB = EC + EB = BC. (1)
+) Chứng minh tương tự với hai tam giác AHM (vuông tại H) và CHM (vuông tại A) có:
AH = CH (giả thiết)
AM là cạnh chung
Suy ra ∆AHM = ∆CHM (hai cạnh góc vuông)
Do đó AM = CM (hai cạnh tương ứng)
Nên MA + MB = MC + MB (2)
+ Xét tam giác BCM có: MC + MB > BC (bất đẳng thức tam giác) (3)
Từ (1), (2) và (3) ta có: MA + MB > EA + EB.
Vậy MA + MB > EA + EB.
Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 3: Hai tam giác bằng nhau
Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh
Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh
Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc
Bài 7: Tam giác cân
Bài 8: Đường vuông góc và đường xiên


