Cho ABC = MNP. Gọi D, E lần lượt là trung điểm của BC và CA; Q, R lần lượt là trung điểm của NP và PM

Bài 4 trang 87 Toán 7 Tập 2: Cho $∆$ABC = $∆$MNP. Gọi D, E lần lượt là trung điểm của BC và CA; Q, R lần lượt là trung điểm của NP và PM. Chứng minh:

a) AD = MQ;

b) DE = QR.

Trả lời

Chứng minh (Hình vẽ dưới đây)

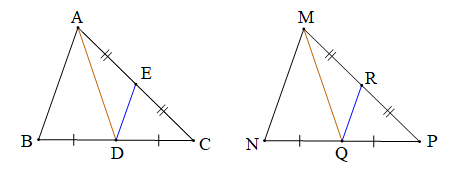
Vì $∆$ABC = $∆$MNP (giả thiết) nên:

+) AC = MP (hai cạnh tương ứng)

+) BC = NP (hai cạnh tương ứng)

+) $\widehat{C}=\widehat{P}$ (hai góc tương ứng)

Vì D là trung điểm của BC (giả thiết) nên BD = DC = $\frac{1}{2}BC$;

E là trung điểm của AC (giả thiết) nên AE = EC = $\frac{1}{2}AC$;

Q là trung điểm của NP (giả thiết) nên NQ = QP = $\frac{1}{2}NP$;

R là trung điểm của MP (giả thiết) nên MR = RP = $\frac{1}{2}MP$.

Do đó ta có BD = DC = NQ = QP và AE = EC = MR = RP.

a) Xét tam giác ADC và tam giác MQP có:

AC = MP (chứng minh trên)

$\widehat{C}=\widehat{P}$ (chứng minh trên)

DC = QP (chứng minh trên)

Suy ra $∆$ADC = $∆$MQP (c.g.c)

Do đó AD = MQ (hai cạnh tương ứng)

Vậy AD = MQ.

b) Xét tam giác CDE và tam giác PQR có:

CD = PQ (chứng minh trên)

$\widehat{C}=\widehat{P}$ (chứng minh trên)

CE = PR (chứng minh trên)

Suy ra $∆$CDE = $∆$PQR (c.g.c)

Do đó DE = QR (hai cạnh tương ứng)

Vậy DE = QR.

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 3: Hai tam giác bằng nhau

Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh

Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc

Bài 7: Tam giác cân

Bài 8: Đường vuông góc và đường xiên