Cho góc xOy có Oz là tia phân giác. Hai điểm M, N lần lượt thuộc Ox, Oy và khác O thoả mãn OM = ON, điểm P khác O và thuộc Oz

Luyện tập 2 trang 85 Toán 7 Tập 2: Cho góc xOy có Oz là tia phân giác. Hai điểm M, N lần lượt thuộc Ox, Oy và khác O thoả mãn OM = ON, điểm P khác O và thuộc Oz. Chứng minh MP = NP.

Trả lời

Chứng minh (Hình vẽ dưới đây)

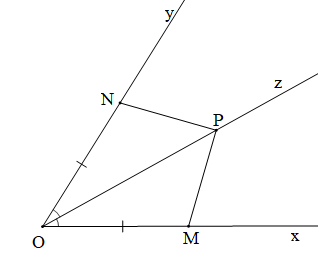
Vì tia Oz là tia phân giác của $\widehat{xOy}$ (giả thiết)

Nên $\widehat{MOP}=\widehat{NOP}$ (tính chất tia phân giác của một góc)

Xét tam giác OMP và tam giác ONP có:

OM = ON (giả thiết)

$\widehat{MOP}=\widehat{NOP}$ (chứng minh trên)

OP là cạnh chung

Suy ra $∆$OMP = $∆$ONP (c.g.c)

Do đó MP = NP (hai cạnh tương ứng)

Vậy MP = NP.

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 3: Hai tam giác bằng nhau

Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh

Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc

Bài 7: Tam giác cân

Bài 8: Đường vuông góc và đường xiên