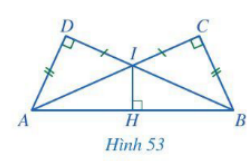
Cho Hình 53 có AD = BC, IC = ID, các góc tại đỉnh C, D, H là góc vuông

Bài 2 trang 86 Toán 7 Tập 2: Cho Hình 53 có AD = BC, IC = ID, các góc tại đỉnh C, D, H là góc vuông.

Chứng minh:

a) IA = IB;

b) IH là tia phân giác của góc AIB.

Trả lời

Chứng minh (Hình 53)

a) Vì $\widehat{C}=\widehat{D}=\widehat{H}=90°$(giả thiết) nên tam giác ADI vuông tại D, tam giác BCI vuông tại C, tam giác AHI và BHI vuông tại H.

Xét tam giác ADI (vuông tại D) và tam giác BCI (vuông tại C) có:

AD = BC (giả thiết)

DI = CI (giả thiết)

Suy ra ∆ADI = ∆BCI (hai cạnh góc vuông)

Suy ra AI = BI (hai cạnh tương ứng)

Vậy AI = BI.

b) Xét tam giác AHI (vuông tại H) và tam giác BHI (vuông tại H) có:

IH là cạnh chung

AI = BI (chứng minh trên)

Suy ra ∆AHI = ∆BHI (cạnh huyền – cạnh góc vuông)

Do đó $\widehat{AIH}=\widehat{BIH}$ (hai góc tương ứng)

Nên tia IH là tia phân giác của góc AIB.

Vậy IH là tia phân giác của góc AIB.

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 3: Hai tam giác bằng nhau

Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh

Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc – cạnh – góc

Bài 7: Tam giác cân

Bài 8: Đường vuông góc và đường xiên