Có bao nhiêu giá trị của tham số m để phương trình x^3 + 3x^2 - m = 0 có hai nghiệm phân biệt

Trả lời

Đáp án B

Phương pháp:

Lập bảng biến thiên của hàm số $y = {x^3} + 3{x^2}$ , từ đó đánh giá m để đồ thị hàm số $y = {x^3} + 3{x^2}$cắt đường thẳng $y = m$ tại 2 điểm phân biệt.

Cách giải:

${x^3} + 3{x^2} - m = 0 \Leftrightarrow {x^3} + 3{x^2} = m\,\,\left( * \right)$

Số nghiệm của phương trình (*) bằng số giao điểm của đồ thị hàm số $y = {x^3} + 3{x^2}$cắt đường thẳng $y = m$.

Xét hàm số $y = {x^3} + 3{x^2}$, ta có $y' = 3{x^2} + 6x;\,\,y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 2\end{array} \right.$

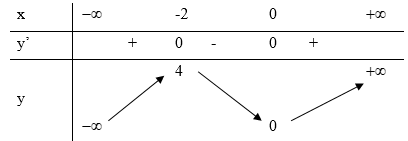
Bảng biến thiên: