Chứng minh rằng với mọi góc α (0° ≤ α ≤ 180°), ta đều có: a) cos^2 α + sin^ 2 α = 1
550
12/06/2023
Bài 5 trang 65 Toán lớp 10 Tập 1: Chứng minh rằng với mọi góc α (0° ≤ α ≤ 180°), ta đều có:
a) cos2α + sin2α = 1;
b) tanα . cotα = 1 (0° < α < 180°, α ≠ 90°).
c) 1 + tan2α = 1cos2α (α ≠ 90°);
d) 1 + cot2 α = 1sin2α (0° < α < 180°).
Trả lời
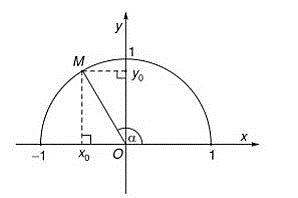
Gọi M là điểm thuộc nửa đường tròn đơn vị sao cho ^xOM=α(00≤α≤1800). Khi đó, ta có:
sinα=y0;cosα=x0,tanα=y0x0;cotα=x0y0
a) cos2α+sin2α=x02+y02=OM2=1. Vậy cos2α+sin2α=1.
b) Với 00<α<1800; α ≠ 900:
tanα. cotα = y0x0.x0y0=1
Vậy tanα. cotα =1 (00<α<1800; α ≠ 900).
c) 1+tan2α=1+sin2αcos2α=cos2α+sin2αcos2α=1cos2α(α≠900).
Vậy 1+tan2α=1cos2α(α≠900).
d) 1+cot2α=1+cos2αsin2α=sin2α+cos2αsin2α=1sin2α(00<α<1800).
Vậy 1+cot2α=1sin2α(00<α<1800).

