Gọi N(x;y) là điểm biểu diễn cho số phức z = x + yi

Ta có $\left|\overline{z}+2-3i\right|\le \left|z-2+i\right|\iff 2x+y+2\le 0$

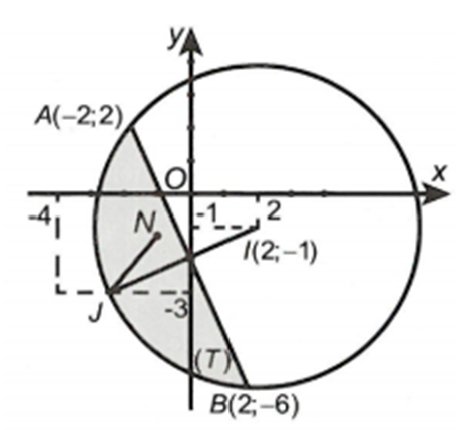
$\left|z-2+i\right|\le 5\iff {\left(x-2\right)}^2+{\left(y+1\right)}^2\le 25$ (hình tròn tâm I(2;-1)  bán kính $r=5$);

Tập hợp các điểm biểu diễn số phức z  thỏa mãn điều kiện $\left|\overline{z}+2-3i\right|\le \left|z-2+i\right|\le 5$ thuộc miền (T) (xem hình vẽ với $A\left(-2;2\right),B\left(2;-6\right)$).

Ta có $P+25={\left(x+4\right)}^2+{\left(y+3\right)}^2$

$\Rightarrow \sqrt{P+25}=\sqrt{{\left(x+4\right)}^2+{\left(y+3\right)}^2}=NJ$ (với J(-4;-3) ) .

Bài toán trở thành tìm điểm N  thuộc miền (T)  sao cho NJ  đạt giá trị lớn nhất, nhỏ nhất.

Ta có $IJ-r\le NJ\le JB\iff 2\sqrt{10}-5\le \sqrt{P+25}\le 3\sqrt{5}\iff 40-20\sqrt{10}\le P\le 20$P đạt giá trị nhỏ nhất khi N là giao điểm của đường thẳng JI với đường tròn tâm I(2;-1)  bán kính r = 5 và $NJ=2\sqrt{10}-5$

P đạt giá trị lớn nhất khi $N\equiv B$

Vậy $m+M=60-20\sqrt{10}$