Chọn B

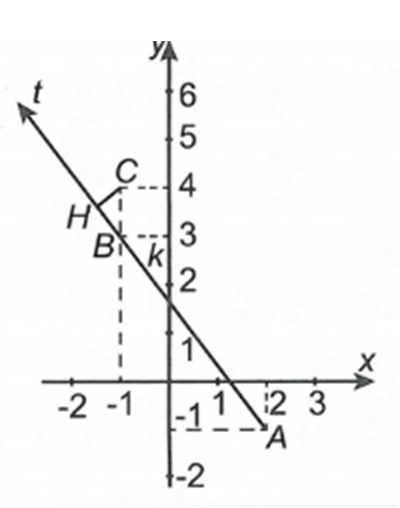
Gọi $M\left(x;y\right)$ là điểm biểu diễn số phức z; gọi $A\left(2;-1\right), B\left(-1;3\right)$ là điểm biểu diễn số phức $2-i; -1+3i$. Ta có AB = 5

Từ giả thiết $\left|z-2+i\right|-\left|z+1-3i\right|=5$

$$\begin{gathered} \Rightarrow \sqrt{{\left(x-2\right)}^2+{\left(y+1\right)}^2}-\sqrt{{\left(x+1\right)}^2+{\left(y-3\right)}^2}=5 \\ \Rightarrow MA-MB=5\Rightarrow MA-MB=AB\Rightarrow MA=MB+AB \end{gathered}$$

Suy ra M, A, B thẳng hàng ( B nằm giữa M và A). Do đó quỹ tích điểm M  là tia Bt  ngược hướng với tia BA

$P=\left|z+1-4i\right|=\sqrt{{\left(x+1\right)}^2+{\left(y-4\right)}^2}$ với $C\left(-1;4\right)\Rightarrow P=MC$

Ta có $\overrightarrow{AB}=\left(-3;4\right)$ phương trình đường thẳng $AB:4x+3y-5=0$

$CH=d\left(C,AB\right)=\frac{\left|4\left(-1\right)+3.4-5\right|}{\sqrt{4^2+3^2}}=\frac{3}{5}, CB=\sqrt{{\left(-1+1\right)}^2+{\left(3-4\right)}^2}=1$

Do đó $\min P=CH=\frac{3}{5}$ khi H là giao điểm của đường thẳng AB và đường thẳng đi qua điểm C và vuông góc với AB