Cho góc xOy. Vẽ cung tròn tâm O, cung này cắt Ox, Oy theo thứ tự tại M, N. Vẽ hai cung tròn tâm M và tâm N có cùng bán kính
383
01/11/2023
Vận dụng 3 trang 54 Toán 7 Tập 2:
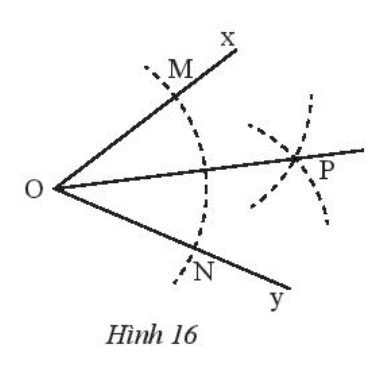
Cho . Vẽ cung tròn tâm O, cung này cắt Ox, Oy theo thứ tự tại M, N. Vẽ hai cung tròn tâm M và tâm N có cùng bán kính sao cho chúng cắt nhau tại điểm P nằm trong Nối O với P (Hình 16). Hãy chứng minh rằng ∆OMP = ∆ONP, từ đó suy ra OP là tia phân giác của .
Trả lời
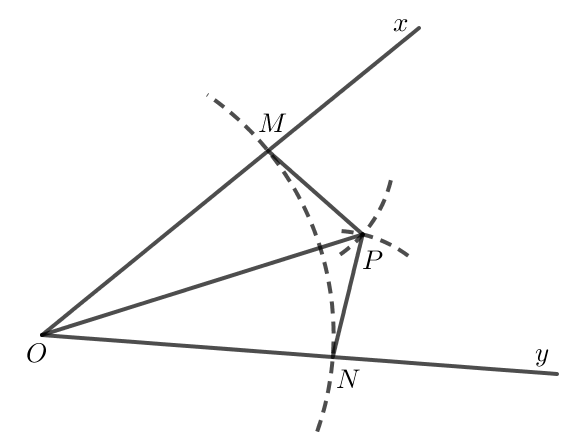
Do M và N cùng thuộc cung tròn tâm O nên OM = ON.
Hai cung tròn tâm M và N có cùng bán kính, cắt nhau tại P nên MP = NP.
Xét ∆OMP và ∆ONP có:
OM = ON (chứng minh trên);
MP = NP (chứng minh trên);
OP là cạnh chung.
Do đó ∆OMP = ∆ONP (c.c.c).
Suy ra (hai góc tương ứng).
Mà OP nằm giữa hai tia Ox và Oy.
Do đó OP là tia phân giác của .
Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài tập cuối chương 7
Bài 1: Góc và cạnh của một tam giác
Bài 2: Tam giác bằng nhau
Bài 3: Tam giác cân
Bài 4: Đường vuông góc và đường xiên
Bài 5: Đường trung trực của một đoạn thẳng


