Cho Hình 25 có EF = HG, EG = HF. Chứng minh rằng: ∆EFH = ∆HGE
Bài 6 trang 58 Toán 7 Tập 2:
Cho Hình 25 có EF = HG, EG = HF. Chứng minh rằng:
a) ∆EFH = ∆HGE.
b) EF // HG.
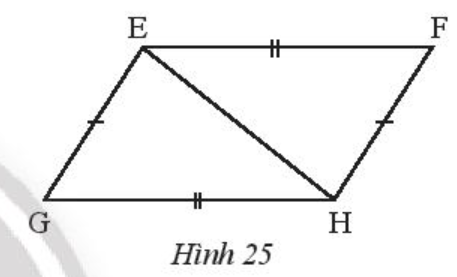
Bài 6 trang 58 Toán 7 Tập 2:
Cho Hình 25 có EF = HG, EG = HF. Chứng minh rằng:
a) ∆EFH = ∆HGE.
b) EF // HG.

a) Xét ∆EFH và ∆HGE có:
EF = HG (giả thiết);
EG = HF (giả thiết);
EH là cạnh chung.
Do đó ∆EFH = ∆HGE (c.c.c).
b) Từ câu a: ∆EFH = ∆HGE.
Suy ra ^FEH=^GHE (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong nên EF // HG.
Vậy EF // HG.
Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Góc và cạnh của một tam giác