Giải SGK Toán 7 (Chân trời sáng tạo): Bài tập cuối chương 7

Giải SGK Toán 7: Bài tập cuối chương 7

Giải Toán 7 trang 42 Tập 2

Bài 1 trang 42 Toán 7 Tập 2:

Cho A = x²y + 2xy - 3y² + 4. Tính giá trị của biểu thức A khi x = -2, y = 3.

Lời giải:

Thay x = -2, y = 3 vào biểu thức A ta được:

A = (-2)² . 3 + 2 . (-2) . 3 - 3 . 3² + 4

= 4 . 3 + (-4) . 3 - 3 . 9 + 4

= 12 - 12 - 27 + 4 = -23.

Vậy khi x = -2, y = 3 thì A = -23.

Bài 2 trang 42 Toán 7 Tập 2:

Trong các biểu thức sau, biểu thức nào là đơn thức một biến?

a) 2y; b) 3x + 5; c) 8; d) 21t¹².

Lời giải:

Các biểu thức 2y; 8; 21t¹² là các đơn thức một biến.

Bài 3 trang 42 Toán 7 Tập 2:

Trong các biểu thức sau, biểu thức nào là đa thức một biến?

3 + 6y; 7x² + 2x - 4x⁴ + 1; $\frac{2}{x+1}$; $\frac{1}{3}$x - 5.

Lời giải:

Các biểu thức 3 + 6y; 7x² + 2x - 4x⁴ + 1; $\frac{1}{3}$x - 5 là các đa thức một biến.

Bài 4 trang 42 Toán 7 Tập 2:

Hãy viết một đa thức một biến bậc ba có 3 số hạng.

Lời giải:

Có rất nhiều cách viết đa thức P(x) là đa thức một biến bậc ba có 3 số hạng.

Chẳng hạn: P(x) = 4x³ + x² – 1.

Bài 5 trang 42 Toán 7 Tập 2:

Hãy cho biết bậc của các đa thức sau:

A = 3x - 4x² + 1;

B = 7;

M = x - 7x³ + 10x⁴ + 2.

Lời giải:

Vì đa thức A có hạng tử bậc cao nhất là -4x² có bậc là 2 nên bậc của đa thức A là 2.

Vì 7 có bậc là 0 nên bậc của đa thức B là 0.

Vì đa thức M có hạng tử bậc cao nhất là 10x⁴ có bậc là 4 nên bậc của đa thức M bằng 4.

Vậy bậc của các đa thức A, B, M lần lượt là bậc 2, bậc 0, bậc 4.

Bài 6 trang 42 Toán 7 Tập 2:

Cho đa thức P(x) = x³ + 27. Tìm nghiệm của P(x) trong tập hợp {0; 3; -3}.

Lời giải:

∙ Với x = 0, ta có P(0) = 0³ + 27 = 27;

∙ Với x = 3, ta có P(3) = 3³ + 27 = 27 + 27 = 54;

∙ Với x = -3, ta có P(-3) = (-3)³ + 27 = (-27) + 27 = 0.

Vậy x = -3 là nghiệm của đa thức P(x).

Bài 7 trang 42 Toán 7 Tập 2:

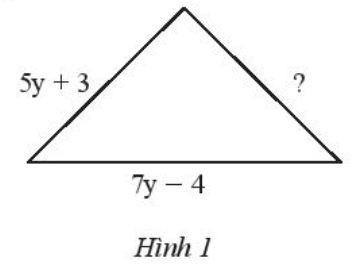
Tam giác trong Hình 1 có chu vi bằng (25y - 8) cm. Tìm cạnh chưa biết trong tam giác đó.

Lời giải:

Chu vi hình tam giác bằng tổng độ dài ba cạnh của tam giác đó.

Khi đó, độ dài cạnh chưa biết là:

(25y - 8) - (5y + 3) - (7y - 4)

= 25y - 8 - 5y - 3 - 7y + 4

= (25y - 5y - 7y) + (-8 - 3 + 4)

= 13y - 7 (cm).

Vậy độ dài cạnh còn lại trong tam giác đó là (13y - 7) cm.

Bài 8 trang 42 Toán 7 Tập 2:

Cho đa thức M(x) = 2x⁴ - 5x³ + 7x² + 3x. Tìm các đa thức N(x), Q(x) sao cho:

N(x) - M(x) = -4x⁴ - 2x³ + 6x² + 7 và Q(x) + M(x) = 6x⁵ - x⁴ + 3x² - 2.

Lời giải:

Ta có N(x) - M(x) = -4x⁴ - 2x³ + 6x² + 7.

Suy ra N(x) = M(x) + (-4x⁴ - 2x³ + 6x² + 7)

= 2x⁴ - 5x³ + 7x² + 3x - 4x⁴ - 2x³ + 6x² + 7

= (2x⁴ - 4x⁴) + (-5x³ - 2x³) + (7x² + 6x²) + 3x + 7

= -2x⁴ - 7x³ + 13x² + 3x + 7

Ta có Q(x) + M(x) = 6x⁵ - x⁴ + 3x² - 2.

Suy ra Q(x) = 6x⁵ - x⁴ + 3x² - 2 - M(x)

= 6x⁵ - x⁴ + 3x² - 2 - (2x⁴ - 5x³ + 7x² + 3x)

= 6x⁵ - x⁴ + 3x² - 2 - 2x⁴ + 5x³ - 7x² - 3x

= 6x⁵ + (-x⁴ - 2x⁴) + 5x³ + (3x² - 7x²) - 3x - 2

= 6x⁵ - 3x⁴ + 5x³ - 4x² - 3x - 2.

Vậy N(x) = -2x⁴ - 7x³ + 13x² + 3x + 7; Q(x) = 6x⁵ - 3x⁴ + 5x³ - 4x² - 3x - 2.

Bài 9 trang 42 Toán 7 Tập 2: Thực hiện phép nhân.

a) (3x - 2)(4x + 5);

b) (x² - 5x + 4)(6x + 1).

Lời giải:

a) Ta có (3x - 2)(4x + 5)

= 3x . 4x + 3x . 5 + (-2) . 4x + (-2) . 5

= 12x² + 15x - 8x - 10

= 12x² + (15x - 8x) - 10

= 12x² + 7x - 10.

Vậy (3x - 2)(4x + 5) = 12x² + 7x - 10.

b) (x² - 5x + 4)(6x + 1)

= x² . 6x + x² . 1 + (-5x) . 6x + (-5x) . 1 + 4 . 6x + 4 . 1

= 6x³ + x²- 30x² - 5x + 24x + 4

= 6x³ + (x² - 30x²) + (-5x + 24x) + 4

= 6x³ - 29x² + 19x + 4.

Vậy (x² - 5x + 4)(6x + 1) = 6x³ - 29x² + 19x + 4.

Bài 10 trang 42 Toán 7 Tập 2: Thực hiện phép chia.

a) (45x⁵ - 5x⁴ + 10x²) : 5x²;

b) (9t² - 3t⁴ + 27t⁵) : 3t.

Lời giải:

a) (45x⁵ - 5x⁴ + 10x²) : 5x²

= (45x⁵ : 5x²) + (-5x⁴ : 5x²) + (10x² : 5x²)

= 9x³ - x² + 2.

Vậy (45x⁵ - 5x⁴ + 10x²) : 5x² = 9x³ - x² + 2.

b) (9t² - 3t⁴ + 27t⁵) : 3t

= (9t² : 3t) + (-3t⁴ : 3t) + (27t⁵ : 3t)

= 3t - t³ + 9t⁴.

Vậy (9t² - 3t⁴ + 27t⁵) : 3t = 3t - t³ + 9t⁴.

Bài 11 trang 42 Toán 7 Tập 2: Thực hiện phép chia.

a) (2y⁴ - 13y³ + 15y² + 11y - 3) : (y² - 4y - 3);

b) (5x³ - 3x² + 10) : (x² + 1).

Lời giải:

a) Thực hiện đặt phép chia, ta được:

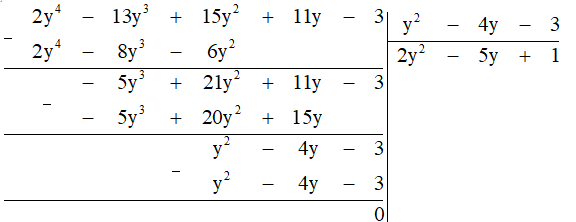
Vậy (2y⁴ - 13y³ + 15y² + 11y - 3) : (y² - 4y - 3) = 2y² - 5y + 1.

b) Thực hiện phép chia, ta được:

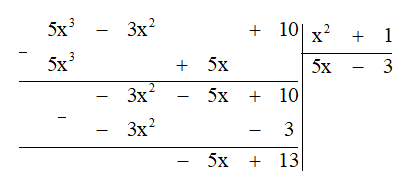
Vậy $\frac{5x^3-3x^2+10}{x^2+1}=5x-3+\frac{-5x+13}{x^2+1}$.

Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

Bài 4: Phép nhân và phép chia đa thức một biến

Bài 5: Hoạt động thực hành và trải nghiệm. Cách tính điểm trung bình môn học kì

Bài 1: Góc và cạnh của một tam giác

Bài 2: Tam giác bằng nhau

Bài 3: Tam giác cân