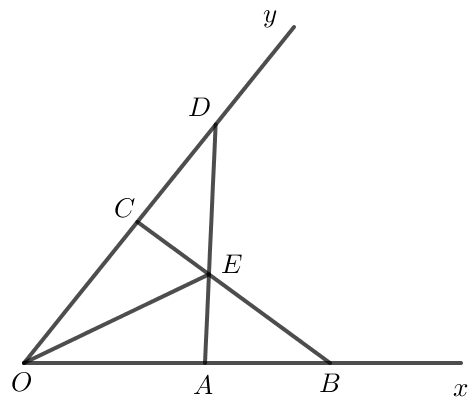
Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB
1.3k
01/11/2023
Bài 8 trang 58 Toán 7 Tập 2:
Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:
a) AD = BC;
b) ∆EAB = ∆ECD;
c) OE là tia phân giác của góc xOy.
Trả lời
a) Xét ∆OAD và ∆OCB có:
OA = OC (giả thiết);
ˆO là góc chung;
OD = OB (giả thiết).
Do đó ∆OAD = ∆OCB (c.g.c).
Suy ra AD = BC (hai cạnh tương ứng).
b) Theo đề bài: OA = OC, OB = OD
Suy ra OB - OA = OD - OC hay AB = CD.
Từ câu a: ∆OAD = ∆OCB.
Suy ra ^ODA=^OBC và ^OAD=^OCB (các cặp góc tương ứng).
Mặt khác: ^OAD+^DAB=180° (hai góc kề bù) và (hai góc kề bù)
Do đó hay .
Xét ∆EAB và ∆ECD có:
(chứng minh trên);
AB = CD (chứng minh trên);
(chứng minh trên).
Do đó ∆EAB = ∆ECD (g.c.g).
c) Từ câu b: ∆EAB = ∆ECD.
Suy ra BE = DE (hai cạnh tương ứng).
Xét ∆ODE và ∆OBE có:
OD = OB (giả thiết);
DE = BE (chứng minh trên);
OE là cạnh chung.
Do đó ∆ODE = ∆OBE (c.c.c).
Suy ra (hai góc tương ứng).
Vậy OE là tia phân giác của .
Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài tập cuối chương 7
Bài 1: Góc và cạnh của một tam giác
Bài 2: Tam giác bằng nhau
Bài 3: Tam giác cân
Bài 4: Đường vuông góc và đường xiên
Bài 5: Đường trung trực của một đoạn thẳng

