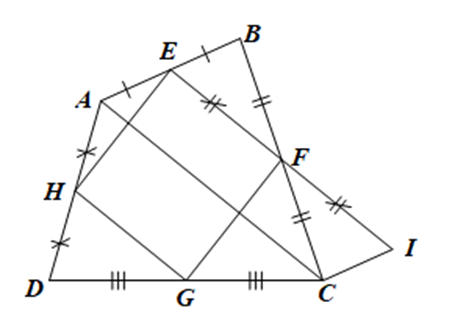
• Gọi I là điểm nằm trên tia đối của tia FE sao cho F là trung điểm của EI.
Tứ giác EBIC có F là trung điểm của BC và EI nên EBIC là hình bình hành
Suy ra BE // CI và BE = CI.
Mà E là trung điểm của AB nên AE = BE, do đó AE = CI
Khi đó tứ giác AEIC có AE // CI và AE = CI nên là hình bình hành
Suy ra EI // AC hay EF // AC.
• Chứng minh tương tự ta cũng có HG // AC, HE // BD, GF // BD
Từ đó ta có được EF // HG và HE // GF
Suy ra tứ giác EFGH là hình bình hành.
• Để hình bình hành EFGH là hình chữ nhật thì ^HEF=90∘ hay HE ⊥ EF
Điều này có nghĩa AC ⊥ BD.
Dễ thấy tứ giác ABCD có AC ⊥ BD thì tứ giác EFGH là hình chữ nhật.
Vậy ta chọn phương án C.