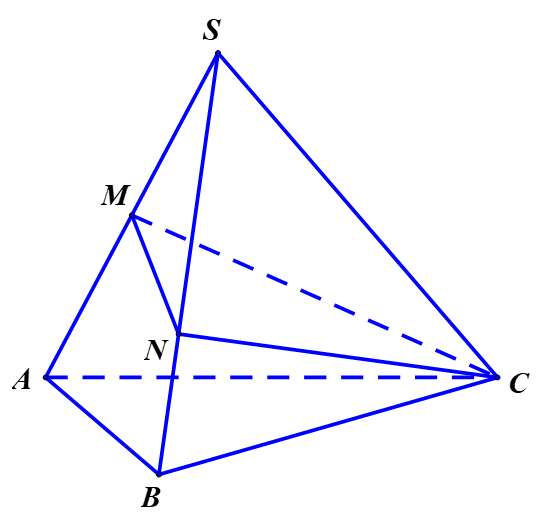
Cho tứ diện SABC, biết vecto SA = 2 vecto SM ;2 vecto SB = 3 vecto SN. Tính thể tích khối tứ diện SMNC biết thể tích khối tứ diện SABC bằng 9. A. 3 B. 4 C. 2 D. 6
41
26/04/2024
Cho tứ diện \(SABC\), biết \(\overrightarrow {SA} = 2\overrightarrow {SM} ;2\overrightarrow {SB} = 3\overrightarrow {SN} \). Tính thể tích khối tứ diện \(SMNC\) biết thể tích khối tứ diện \(SABC\) bằng \(9.\)
A. \(3\)
B. \(4\)
C. \(2\)
D. \(6\)
Trả lời
Lời giải
Chọn A.
Ta có \(\overrightarrow {SA} = 2\overrightarrow {SM} \) nên \(M\) là trung điểm của \(SA\)và \(2.\overrightarrow {SB} = 3\overrightarrow {SN} \) nên chia \(SB\) thành 3 phân sao cho \(\frac{{SN}}{{SB}} = \frac{2}{3}\).
Khi đó, theo công thức tỉ lệ thể tích ta có:
\[\frac{{{V_{S.MNC}}}}{{{V_{S.ABC}}}} = \frac{{SM}}{{SA}}.\frac{{SN}}{{SB}}.\frac{{SC}}{{SC}} = \frac{1}{2}.\frac{2}{3}.1 = \frac{1}{3} \Rightarrow {V_{S.MNC}} = \frac{1}{3}{V_{S.ABC}} = \frac{1}{3}.9 = 3\,\,\,(DVTT)\]
