Cho tứ diện OABC có OA vuông góc với mặt phẳng (OBC) và có A′, B′, C′ lần lượt là trung điểm

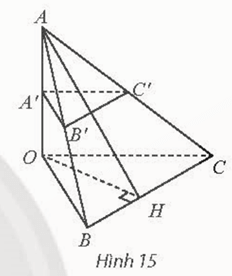
Thực hành 2 trang 61 Toán 11 Tập 2: Cho tứ diện OABC có OA vuông góc với mặt phẳng (OBC) và có A′, B′, C′ lần lượt là trung điểm của OA, OB, OC. Vẽ OH là đường cao của tam giác OBC. Chứng minh rằng:

a) OA ⊥ (A ′B′C′) ;

b) B′ C′ ⊥ (OAH ).

Trả lời

a) Xét tam giác OAB:

A′ là trung điểm OA

B′ là trung điểm AB

Nên A ′B′ là đường trung bình của ΔOAB.

Do đó A ′B′ // OB ⇒ A ′B′ // (OBC) (vì $\left(\mathrm{OB}\subset \left(\mathrm{OBC}\right)\right)$

Tương tự: B′C′ là đường trung bình của ΔABC

Do đó B ′C′ // BC ⇒ B ′C′ // (OBC) (vì $\left(\mathrm{BC}\subset \left(\mathrm{OBC}\right)\right)$

Ta có:

$\left.\begin{array}{c}{\mathrm{A}}^{\text{'}}\text{\hspace{0.17em}//\hspace{0.17em}}\left(\mathrm{OBC}\right)\\ {\mathrm{B}}^{\text{'}}{\mathrm{C}}^{\text{'}}\text{\hspace{0.17em}//}\left(\mathrm{OBC}\right)\\ {\mathrm{A}}^{\text{'}},\mathrm{B}\text{'}\mathrm{C}\text{'}\subset \left({\mathrm{A}}^{\text{'}}{\mathrm{B}}^{\text{'}}{\mathrm{C}}^{\text{'}}\right)\end{array}\right\}\Rightarrow \left({\mathrm{A}}^{\text{'}}{\mathrm{B}}^{\text{'}}{\mathrm{C}}^{\text{'}}\right)\text{\hspace{0.17em}//}\left(\text{OBC}\right)$

Mà OA ⊥ (OBC)

Vậy OA ⊥ (A ′B′C′).

b) Ta có OA ⊥ (OBC) nên OA ⊥ BC

M à OH ⊥ BC (OH là đường cao của ΔOBC) , suy ra BC ⊥ (OAH)

Lại có: B′C′ // BC nên B ′C′ ⊥ (OAH).

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác: