Giải SGK Toán 11 (Chân trời sáng tạo) Bài 1: Hai đường thẳng vuông góc

Giải Toán 11 Bài 1: Hai đường thẳng vuông góc

Hoạt động khởi động trang 54 Toán 11 Tập 2: Ta đã biết cách xác định góc giữa hai đường thẳng cùng thuộc một mặt phẳng. Có góc giữa hai đường thẳng chéo nhau không? Nếu có, làm thế nào để xác định?

Lời giải:

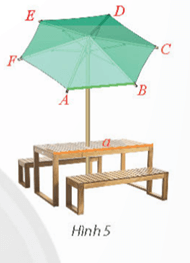
Sau khi học xong bài học này, ta giải quyết bài toán trên như sau:

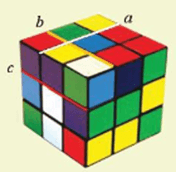
Có góc giữa 2 đường thẳng chéo nhau.

Cách xác định góc giữa hai đường thẳng chéo nhau a và b: Kẻ một đường thẳng c song song với b thuộc mặt phẳng chứa a. Góc giữa a và b bằng góc giữa a và c.

1. Góc giữa hai đường thẳng trong không gian

Hoạt động khám phá 1 trang 54 Toán 11 Tập 2: Cho hai đường thẳng chéo nhau a và b trong không gian. Qua một điểm M tuỳ ý vẽ a // a′ và vẽ b // b′. Khi thay đổi vị trí của điểm M, có nhận xét gì về góc giữa a′ và b′?

Lời giải:

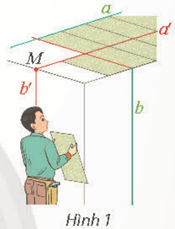
Khi thay đổi vị trí của điểm M , g óc giữa a′ và b ′ không thay đổi.

2. Hai đường thẳng vuông góc trong không gian

Thực hành 1 trang 55 Toán 11 Tập 2: Cho hình hộp ABCD.A′B′C′D′ có 6 mặt đều là hình vuông M, N, E, F lần lượt là trung điểm các cạnh BC, BA, AA′, A′D′. Tính góc giữa các cặp đường thẳng:

a) MN và DD ′ ;

b) MN và CD ′ ;

c) EF và CC ′ .

Lời giải:

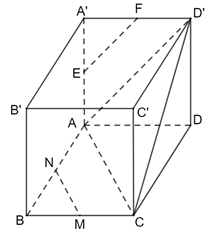
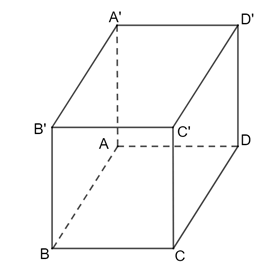
a) Xét tam giác ABC có:

M là trung điểm của BC

N là trung điểm của BA

Nên MN là đường trung bình của tam giác ABC.

⇒ MN // AC

Mà DD ′ // AA ′ nên (MN, DD ′ ) = (AC, AA ′ ) = $\widehat{A^{\text{'}}\mathrm{AC}}=90°$

b) Ta có: MN // AC

⇒ (MN, CD ′ ) = (AC, CD ′ ) = $\widehat{{\mathrm{ACD}}^{\text{'}}}$

Vì ABCD, ADD ′A′, CDD′C′ là các hình vuông bằng nhau nên các đường chéo của chúng bằng nhau nên AC = AD′ = CD′.

Suy ra ACD ′ là tam giác đều.

⇒ $$ $\widehat{{\mathrm{ACD}}^{\text{'}}}={60}^o$ hay (MN, CD ′ ) = 60 °

c) Xét tam giác AA′D′ có:

E là trung điểm của AA ′

F là trung điểm của A ′D′

Nên EF là đường trung bình của tam giác AA ′D′ .

⇒ EF // AD ′

Mà CC ′ // AA ′

⇒ (EF, CC ′ ) = (AD ′ , AA ′ ) = $\widehat{A^{\text{'}}{\mathrm{AD}}^{\text{'}}}=45°$

Vận dụng 1 trang 55 Toán 11 Tập 2: Khung của một mái nhà được ghép bởi các thanh gỗ như Hình 3. Cho biết tam giác OMN vuông cân tại O. Tính góc giữa hai thanh gỗ a và b.

Lời giải:

Vì a // OM nên (a, b) = (MN, OM) = $\widehat{\mathrm{OMN}}$.

Mà tam giác OMN vuông cân tại O. Vậy góc giữa a và b là 45 °.

Hoạt động khám phá 2 trang 55 Toán 11 Tập 2: Cho hình hộp ABCD.A′B′C′D′ có 6 mặt đều là hình vuông. Nêu nhận xét về góc giữa các cặp đường thẳng:

a) AB và BB′ ;

b) AB và DD′ .

Lời giải:

a) ABB′A′ là hình vuông nên AB ⊥ BB ′ hay góc giữa AB và BB′ là 90 °.

b) Vì DD′ // AA′ nên (AB, DD′) = (AB, AA′) = $\widehat{A^{\text{'}}\mathrm{AB}}=90°$ .

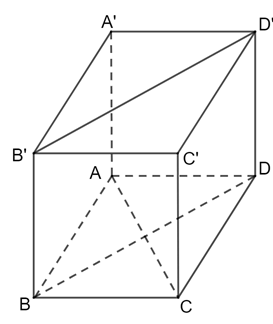
Thực hành 2 trang 55 Toán 11 Tập 2: Cho hình hộp ABCD.A′B′C′D′ có 6 mặt đều là hình vuông.

a) Tìm các đường thẳng đi qua hai đỉnh của hình lập phương và vuông góc với AC .

b) Trong các đường thẳng tìm được ở câu a, tìm đường thẳng chéo với AC .

Lời giải:

a) Các đường thẳng đi qua hai đỉnh của hình hộp và vuông góc với AC là BD, B′D′, AA′, CC′, BB′, DD′.

b) Trong các đường thẳng trên, đường thẳng chéo với AC là B′D′.

Vận dụng 2 trang 55 Toán 11 Tập 2: Hình bên mô tả một người thợ đang ốp gạch vào tường có sử dụng thước laser để kẻ vạch. Tìm các đường thẳng vuông góc với đường thẳng a trong Hình 4.

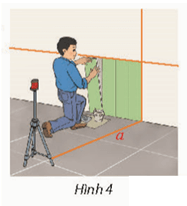
Lời giải:

Các đường thẳng vuông góc với a là: chân tường, mép các viên gạch ốp tường, mép các viên gạch sàn nhà song song với chân tường, …

Bài tập

Bài 1 trang 56 Toán 11 Tập 2: Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a. Cho biết SA = $\text{a}\sqrt{3}$ , SA ⊥AB và SA ⊥AD. Tính góc giữa SB và CD, SD và CB.

Lời giải:

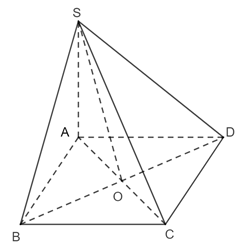
Vì CD // AB nên (SB, CD) = (SB, AB) = $\widehat{\mathrm{SBA}}$

Xét tam giác SBA có: SA ⊥AB nên ΔSAB vuông tại A.

$\tan \widehat{\mathrm{SBA}}=\frac{\mathrm{SA}}{\mathrm{AB}}=\frac{a\sqrt{3}}{a}=\sqrt{3}$. Vậy $\widehat{\mathrm{SBA}}=60°$ .

Mặt khác, CB // AD nên (SD, CB) = (SD, AD) = $\widehat{\mathrm{SDA}}$

Xét tam giác SDA có: SD⊥AD nên ΔSDA vuông tại D.

$\tan \widehat{\mathrm{SDA}}=\frac{\mathrm{SA}}{\mathrm{AD}}=\frac{a\sqrt{3}}{a}=\sqrt{3}$.

Vậy $\widehat{\mathrm{SDA}}=60°$.

Bài 2 trang 56 Toán 11 Tập 2: Cho tứ diện đều ABCD. Chứng minh rằng AB ⊥ CD.

Lời giải:

Gọi a là độ dài cạnh của tứ diện đều ABCD.

Gọi M, N, P lần lượt là trung điểm của các cạnh AC, BC và AD.

Xét tam giác ABC:

M là trung điểm của AC.

N là trung điểm của BC.

Nên MN là đường trung bình của tam giác ABC.

⇒ MN // AB; MN = $\frac{1}{2}$AB = $\frac{a}{2}$ (1)

Tương tự: MP là đường trung bình tam giác ACD:

⇒ MP // CD; MP = $\frac{1}{2}$CD = $\frac{a}{2}$ (2)

Từ (1) và (2) ⇒ MN = MP = $\frac{a}{2}$

Tam giác ABD đều có BP là trung tuyến nên BP = $\frac{a\sqrt{3}}{2}$

Tam giác ACD đều có CP là trung tuyến nên CP = $\frac{a\sqrt{3}}{2}$

Xét tam giác BCP có: BP = CP = $\frac{a\sqrt{3}}{2}$

⇒ Tam giác BCP cân tại P.

Mà N là trung điểm của BC ⇒ PN là đường trung tuyến nên PN ⊥ CN

PN = $\sqrt{{\mathrm{CP}}^2-{\mathrm{CN}}^2}=\sqrt{{\left(\frac{a\sqrt{3}}{2}\right)}^2-{\left(\frac{a}{2}\right)}^2}=\frac{a\sqrt{2}}{2}$

Xét tam giác MNP:

MP² + MN² = ${\left(\frac{a}{2}\right)}^2+{\left(\frac{a}{2}\right)}^2=\frac{2a^2}{4}$ ; PN² = ${\left(\frac{a\sqrt{2}}{2}\right)}^2=\frac{2a^2}{4}$

⇒ MP² + MN² = PN²

⇒ Tam giác MNP vuông tại M.

Ta có: (AB, CD) = (MN, MP) = $\widehat{\mathrm{NMP}}=90°$.

Vậy AB ⊥CD.

Bài 3 trang 56 Toán 11 Tập 2: Cho hình chóp S.ABC có SA = SB = SC = a, $\widehat{\mathrm{BSA}}=\widehat{\mathrm{CSA}}=60°,\widehat{\mathrm{BSC}}=90°.$ Cho I và J lần lượt là trung điểm của SA và BC. Chứng minh rằng IJ ⊥SA và IJ ⊥BC.

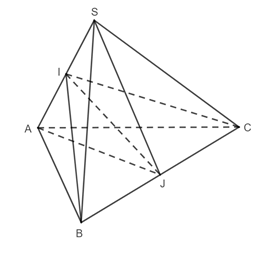
Lời giải:

Xét tam giác SAB có:

SA = SB = a

$\widehat{\mathrm{BSA}}=60°$

⇒ $$Tam giác SAB đều.

Mà I là trung điểm của SA ⇒ $$IB = $\frac{a\sqrt{3}}{2}$

Xét tam giác SAC có:

SA = SC = a

$\widehat{\mathrm{ASC}}=60°$

⇒ $$Tam giác SAC đều.

Mà I là trung điểm của SA ⇒ $$IC = $\frac{a\sqrt{3}}{2}$

Ta có BSC là tam giác vuông cân tại S.

⇒ $\text{BC}=\sqrt{{\text{SB}}^2+{\text{SC}}^2}=a\sqrt{2}$

Xét tam giác ABC:

AB = AC = a

AB² + AC² = a² + a² = 2a²

BC² = ${\left(a\sqrt{2}\right)}^2$= 2a²

⇒ $$AB² + AC² = BC²

⇒ Tam giác ABC vuông cân tại A.

Mà J là trung điểm đoạn BC ⇒ AJ ⊥ BC

⇒ $$ AJ = $\sqrt{{\text{AB}}^2-{\text{BJ}}^2}=\sqrt{a^2-{\left(\frac{a\sqrt{2}}{2}\right)}^2}=\frac{a\sqrt{2}}{2}$

Xét tam giác SBC vuông cân tại S:

Mà J là trung điểm đoạn BC ⇒ $$ SJ ⊥ BC

⇒ $$ SJ = $\sqrt{{\text{SB}}^2-{\text{BJ}}^2}=\sqrt{a^2-{\left(\frac{a\sqrt{2}}{2}\right)}^2}=\frac{a\sqrt{2}}{2}$

Xét tam giác JSA:

AJ = SJ = $\frac{a\sqrt{2}}{2}$

⇒ $$ Tam giác JSA cân tại J.

Mà I là trung điểm của SA ⇒ IJ là đường trung tuyến của tam giác JSA.

hay IJ ⊥SA.

Xét tam giác IBC:

IB = IC = $\frac{a\sqrt{3}}{2}$

⇒ $$Tam giác IBC cân tại I.

Mà J là trung điểm của BC ⇒ $$ IJ là đường trung tuyến của tam giác IBC.

hay IJ ⊥BC.

Bài 4 trang 56 Toán 11 Tập 2: Cho tứ diện đều ABCD cạnh a. Gọi K là trung điểm CD. Tính góc giữa hai đường thẳng AK và BC.

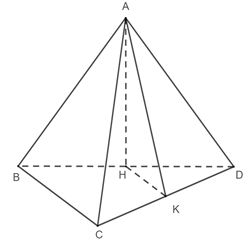
Lời giải:

Gọi H là trung điểm của BD.

Ta có: K là trung điểm của CD.

Nên HK là đường trung bình tam giác BCD

⇒ HK // BC; HK = $\frac{1}{2}\mathrm{BC}=\frac{a}{2}$

⇒ (AK, BC) = (AK, HK)

Xét tam giác ABC đều có H là trung điểm của BC ⇒ $$ AH = $\frac{a\sqrt{3}}{2}$

Xét tam giác ACD đều có K là trung điểm của CD ⇒ $$ AK = $\frac{a\sqrt{3}}{2}$

Xét tam giác AHK: $\text{cos}\widehat{\mathrm{AKH}}=\frac{{\mathrm{AK}}^2+{\mathrm{HK}}^2-{\mathrm{AH}}^2}{2.\mathrm{AK}.\mathrm{HK}}=\frac{\sqrt{3}}{6}$

⇒ $\widehat{\mathrm{AKH}}\approx 73,2°$

Vậy (AK, BC) = $\widehat{\mathrm{AKH}}\approx 73,2°$

Bài 5 trang 56 Toán 11 Tập 2: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của BC và AD. Biết AB = CD = 2a và MN = $\mathrm{a}\sqrt{3}$ . Tính góc giữa AB và CD.

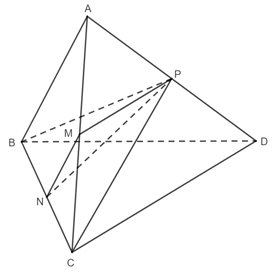
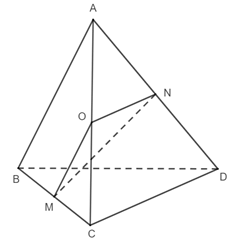
Lời giải:

Gọi O là trung điểm của AC.

Ta có M là trung điểm của BC.

⇒ $$OM là đường trung bình tam giác ABC

⇒ $$OM // AB; OM = $\frac{1}{2}$ AB = a

Tương tự ON là đường trung bình tam giác ACD.

⇒ $$ ON // CD; ON = $\frac{1}{2}$CD = a

⇒ $$ (AB, CD) = (OM, ON)

Trong tam giác MON:

OM = ON = a; MN = $a\sqrt{3}$

$\cos \widehat{\mathrm{MON}}=\frac{{\mathrm{OM}}^2+{\mathrm{ON}}^2-{\mathrm{MN}}^2}{2.\mathrm{OM}.\mathrm{ON}}=\frac{a^2+a^2-{\left(a\sqrt{3}\right)}^2}{2.a.a}=\frac{-1}{2}$

⇒ $\widehat{\mathrm{MON}}=120°$.

Vậy $(\mathrm{AB},\mathrm{CD})=180°-\widehat{\mathrm{MON}}=60°$.

Bài 6 trang 56 Toán 11 Tập 2: Một ô che nắng có viền khung hình lục giác đều ABCDEF song song với mặt bàn và có cạnh AB song song với cạnh bàn a (Hình 5). Tính số đo góc hợp bởi đường thẳng a lần lượt với các đường thẳng AF, AE và AD.

Lời giải:

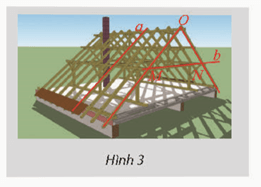
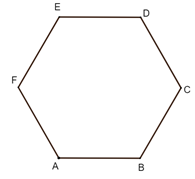
Ta có: AB // a, nên

(a, AF) = (AB, AF) = 120°

(a, AE) = (AB, AE) = 90°

(a, AD) = (AB, AD) = 60°

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác: