Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = a và OC = 2a

Bài 7.38 trang 65 Toán 11 Tập 2: Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = a và OC = 2a. Tính khoảng cách từ điểm O đến mặt phẳng ABC.

Trả lời

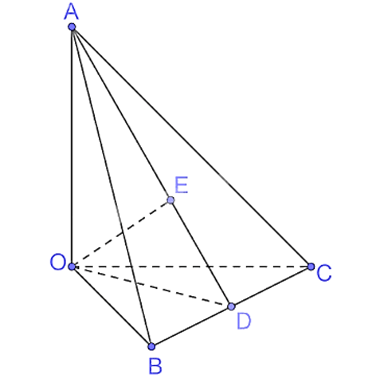
Kẻ OD $\perp$ BC tại D.

Có OA $\perp$ OB, OA $\perp$ OC nên OA $\perp$ (OBC), suy ra OA $\perp$ BC mà OD $\perp$ BC nên

BC $\perp$ (OAD).

Kẻ OE $\perp$ AD tại E.

Vì BC $\perp$ (OAD) nên BC $\perp$ OE mà OE $\perp$ AD nên OE $\perp$ (ABC).

Do đó d(O, (ABC)) = OE.

Xét tam giác OBC vuông tại O, OD là đường cao có:

$\frac{1}{O{D}^2}=\frac{1}{O{B}^2}+\frac{1}{O{C}^2}$$=\frac{1}{2a^2}+\frac{1}{4a^2}=\frac{3}{4a^2}$.

Vì OA $\perp$ (OBC) nên OA $\perp$ OD.

Xét tam giác AOD vuông tại O, OE là đường cao nên

$\frac{1}{O{E}^2}=\frac{1}{O{A}^2}+\frac{1}{O{D}^2}$$=\frac{1}{a^2}+\frac{3}{4a^2}=\frac{7}{4a^2}$$\Rightarrow OE=\frac{2a\sqrt{7}}{7}$.

Vậy d(O, (ABC))$=\frac{2a\sqrt{7}}{7}$.

Xem thêm các bài giải SGK Toán lớp 11 Kết nối tri thức hay, chi tiết khác: