Giải SGK Toán 11 (Kết nối tri thức) Bài 30: Công thức nhân xác suất cho hai biến cố độc lập

Giải Toán 11 Bài 30: Công thức nhân xác suất cho hai biến cố độc lập

Mở đầu trang 76 Toán 11 Tập 2: Tại vòng chung kết của một đại hội thể thao, vận động viên An thi đấu môn Bắn súng, vận động viên Bình thi đấu môn Bơi lội. Biết rằng xác suất giành huy chương của vận động viên An và vận động viên Bình tương ứng là 0,8 và 0,9. Hỏi xác suất để cả hai vận động viên đạt huy chương là bao nhiêu ?

Lời giải:

Sau bài học, ta trả lời được như sau:

Xác suất để cả hai vận động viên đạt huy chương là: 0,8 . 0,9 = 0,72.

1. Công thức nhân xác suất cho hai biến cố độc lập

HĐ1 trang 76 Toán 11 Tập 2: Có hai hộp đựng các quả bóng có cùng kích thước và khối lượng. Hộp I có 6 quả màu trắng và 4 quả màu đen. Hộp II có 1 quả màu trắng và 7 quả màu đen. Bạn Long lấy ngẫu nhiên một quả bóng từ hộp I, bạn Hải lấy ngẫu nhiên một quả bóng từ hộp II. Xét các biến cố sau:

A: “Bạn Long lấy được quả bóng màu trắng”;

B: “Bạn Hải lấy được quả bóng màu đen”.

a) Tính P(A), P(B) và P(AB).

b) So sánh P(AB) và P(A) . P(B).

Lời giải:

a)

+ Tính P(A):

Biến cố A là tập hợp các quả màu trắng trong 10 quả của hộp I nên n(A) = 6.

Suy ra: P(A) = $\frac{6}{10}$ .

+ Tính P(B)

Biến cố B là tập hợp các quả màu đen trong 8 quả của hộp II nên n(B) = 7.

Suy ra: P(B) = $\frac{7}{8}$ .

+ Tính P(AB):

Biến cố C = A ∩ B là biến cố “Bạn Long lấy được quả màu trắng và bạn Hải lấy được quả màu đen”.

Không gian mẫu Ω là tập hợp các cách chọn gồm 2 công đoạn:

Công đoạn 1: Bạn Long lấy ngẫu nhiên một quả bóng từ hộp I.

Có 6 + 4 = 10 (cách chọn).

Công đoạn 2: Bạn Hải lấy ngẫu nhiên một quả bóng từ hộp II.

Có 1 + 7 = 8 (cách chọn)

Theo quy tắc nhân, ta có: n(Ω) = 10 . 8 = 80.

Biến cố C là tập hợp các cách chọn gồm 2 công đoạn:

Công đoạn 1: Bạn Long lấy được quả màu trắng trong hộp I. Có 6 cách chọn.

Công đoạn 2: Bạn Hải lấy được quả màu đen trong hộp II. Có 7 cách chọn.

Theo quy tắc nhân, ta có: n(C) = 6 . 7 = 42.

Suy ra: P(AB) = P(C) = $\frac{42}{80}=\frac{21}{40}$ .

b)

Ta có: P(A) . P(B) = $\frac{6}{10}.\frac{7}{8}=\frac{21}{40}$ .

Như vậy P(A) . P(B) = P(AB).

Câu hỏi trang 76 Toán 11 Tập 2: Hai biến cố A và B trong HĐ1 độc lập hay không độc lập ? Tại sao ?

Lời giải:

Vì Long và Hải lấy bóng từ hai hộp khác nhau nên:

Dù biến cố A có xảy ra hay không ta đều có P(B) = $\frac{7}{8}$ .

Dù biến cố B có xảy ra hay không ra đều có P(A) = $\frac{6}{10}$ .

Vậy hai biến cố A và B độc lập.

Luyện tập 1 trang 77 Toán 11 Tập 2: Các học sinh lớp 11D làm thí nghiệm gieo hai loại hạt giống A và B. Xác suất để hai loại hạt giống A và B nảy mầm tương ứng là 0,92 và 0,88. Giả sử việc nảy mầm của hạt A và hạt B là độc lập với nhau. Dùng sơ đồ hình cây tính xác suất để:

a) Hạt giống A nảy mầm còn hạt giống B không nảy mầm;

b) Hạt giống A không nảy mầm còn hạt giống B nảy mầm;

c) Ít nhất có một trong hai loại hạt giống nảy mầm

Lời giải:

Gọi A là biến cố “Hạt giống A nảy mầm”; B là biến cố “Hạt giống B nảy mầm”.

Các biến cố đối $\overline{A}$ là biến cố “Hạt giống A không nảy mầm”; $\overline{B}$ là “Hạt giống B không nảy mầm”.

Ta có:

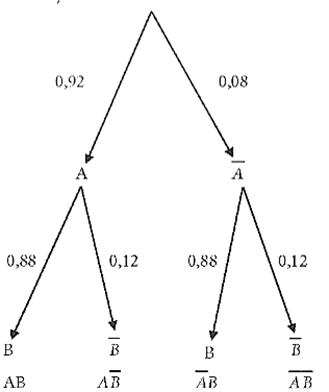
P(A) = 0,92. Suy ra P($\overline{A}$) = 1 – 0,92 = 0,08.

P(B) = 0,88. Suy ra P($\overline{B}$) = 1 – 0,88 = 0,12.

Ta có sơ đồ hình cây như sau:

Ta có hai biến cố A và B độc lập.

a)

Biến cố: “Hạt giống A nảy mầm còn hạt giống B không nảy mầm” là biến cố A$\overline{B}$.

Áp dụng công thức nhân xác suất, ta có:

P(A$\overline{B}$) = P(A) . P($\overline{B}$) = 0,92 . 0,12 = 0,1104.

b)

Biến cố: “Hạt giống A không nảy mầm còn hạt giống B nảy mầm” là biến cố $\overline{A}$ B.

Áp dụng công thức nhân xác suất, ta có:

P($\overline{A}$B) = P($\overline{A}$) . P(B) = 0,08 . 0,88 = 0,0704.

c)

Biến cố: “Có ít nhất một trong hai loại hạt giống nảy mầm” là biến cố A ∪ B.

Áp dụng công thức cộng xác suất và công thức nhân xác suất, ta có:

P(A ∪ B) = P(A) + P(B) – P(AB)

= P(A) + P(B) – P(A) . P(B)

= 0,92 + 0,88 – 0,92 . 0,88

= 0,9904.

Vậy P(A ∪ B) = 0,9904.

2. Vận dụng

Luyện tập 2 trang 78 Toán 11 Tập 2: Để nghiên cứu mối liên quan giữa thói quen hút thuốc lá với bệnh viêm phổi, nhà nghiên cứu chọn một nhóm 5 000 người đàn ông. Với mỗi người trong nhóm, nhà nghiên cứu kiểm tra xem họ có nghiện thuốc lá và có bị viêm phổi hay không. Kết quả được thống kê trong bảng sau:

Từ bảng thống kê trên, hãy chứng tỏ rằng việc nghiện thuốc lá và mắc bệnh viêm phổi có liên quan với nhau.

Lời giải:

Chọn ngẫu nhiên một người đàn ông.

Gọi A là biến cố “Người đó nghiện thuốc lá”,

B là biến cố “Người đó mắc bệnh viêm phổi”.

Khi đó, AB là biến cố “Người đó nghiện thuốc lá và mắc bệnh viêm phổi”.

Ta có: P(A) = $\frac{752+1236}{5000}=\frac{497}{1250}$ ; P(B) = $\frac{752+575}{5000}=\frac{1327}{5000}$

Suy ra: P(A) . P(B) = $\frac{497}{1250}.\frac{1327}{5000}$ = 0,10552304

Mặt khác số người nghiện thuốc là và mắc bệnh viêm phổi là 752 nên

P(AB) = $\frac{752}{5000}$ = 0,1504.

Do đó, P(AB) ≠ P(A) . P(B) nên hai biến cố A và B không độc lập.

Vậy ta kết luận rằng việc nghiện thuốc lá và mắc bệnh viêm phổi có liên quan với nhau.

Bài tập

Bài 8.11 trang 78 Toán 11 Tập 2: Cho hai biến cố A và B là hai biến cố xung khắc với P(A) > 0, P(B) > 0. Chứng tỏ rằng hai biến cố A và B không độc lập.

Lời giải:

Hai biến cố A và B xung khắc khi và chỉ khi A ∩ B = ∅. Suy ra: P(AB) = 0.

Vì P(A) > 0, P(B) > 0 nên P(A) . P(B) > 0.

Do đó, P(AB) ≠ P(A) . P(B)

Vậy hai biến cố A và B không độc lập.

Bài 8.12 trang 78 Toán 11 Tập 2: Một thùng đựng 60 tấm thẻ cùng loại được đánh số từ 1 đến 60. Rút ngẫu nhiên một tấm thẻ trong thùng. Xét hai biến cố sau:

A: “Số ghi trên tấm thẻ là ước của 60” và B: “Số ghi trên tấm thẻ là ước của 48”.

Chứng tỏ rằng A và B là hai biến cố không độc lập.

Lời giải:

Ta có:

A = {1; 2; 3; 4; 5; 6; 10; 12; 15; 20; 30; 60}

B = {1; 2; 3; 4; 6; 8; 12; 16; 24; 48}

Do đó, AB = A ∩ B = {1; 2; 3; 4; 6; 12}.

Suy ra

P(A) = $\frac{12}{60}=\frac{1}{5}$; P(B) = $\frac{10}{60}=\frac{1}{6}$ ; P(AB) = $\frac{6}{60}=\frac{1}{10}$ .

Mặt khác, P(A) . P(B) = $\frac{1}{5}.\frac{1}{6}=\frac{1}{30}$ .

Khi đó P(AB) ≠ P(A) . P(B) nên hai biến cố A và B không độc lập.

Bài 8.13 trang 78 Toán 11 Tập 2: Có hai túi đựng các viên bi có cùng kích thước và khối lượng. Túi I có 3 viên bi màu xanh và 7 viên bi màu đỏ. Túi II có 10 viên bi màu xanh và 6 viên bi màu đỏ. Từ mỗi túi, lấy ngẫu nhiên ra một viên bi. Tính xác suất để:

a) Hai viên bi được lấy có cùng màu xanh;

b) Hai viên bi được lấy có cùng màu đỏ;

c) Hai viên bi được lấy có cùng màu;

d) Hai viên bi được lấy không cùng màu.

Lời giải:

Vì hai túi là khác nhau nên biến cố lấy một viên bi mỗi túi là độc lập.

Gọi biến cố A: “Hai viên bi được lấy có cùng màu xanh”;

B là biến cố “Hai viên bi được lấy có cùng màu đỏ”;

C là biến cố “Hai viên bi được lấy có cùng màu”.

a)

Xác suất lấy được viên bi màu xanh từ túi I là: $\frac{3}{10}$ .

Xác suất lấy được viên bi màu xanh từ túi II là: $\frac{10}{16}=\frac{5}{8}$ .

Theo quy tắc nhân, xác suất lấy được hai viên bi cùng màu xanh là:

P(A) = $\frac{3}{10}.\frac{5}{8}=\frac{3}{16}$ .

b)

Xác suất lấy được viên bi màu đỏ từ túi I là: $\frac{7}{10}$ .

Xác suất lấy được viên bi màu đỏ từ túi II là: $\frac{6}{16}=\frac{3}{8}$ .

Theo quy tắc nhân, xác suất lấy được hai viên bi cùng màu đỏ là:

P(B) = $\frac{7}{10}.\frac{3}{8}=\frac{21}{80}$ .

c)

Ta có C = A ∪ B mà A và B xung khắc nên áp dụng công thức cộng xác suất:

P(C) = P(A ∪ B) = P(A) + P(B) = $\frac{3}{16}+\frac{21}{80}=\frac{9}{20}$ .

Vậy xác suất để hai viên bi được lấy có cùng màu là: $\frac{9}{20}$ .

d) Gọi biến cố D: “Hai viên bi được lấy không cùng màu”.

Khi đó, $\overline{D}$=C.

Suy ra: P(D) = 1 – P($\overline{D}$) = 1 – P(C) = 1 – $\frac{9}{20}$ = $\frac{11}{20}$ .

Vậy xác suất để hai viên bi được lấy không cùng màu là $\frac{11}{20}$.

Bài 8.14 trang 78 Toán 11 Tập 2: Có hai túi mỗi túi đựng 10 quả cầu có cùng kích thước và khối lượng được đánh số từ 1 đến 10. Từ mỗi túi, lấy ngẫu nhiên ra một quả cầu. Tính xác suất để trong hai quả cầu được lấy ra không có quả cầu nào ghi số 1 hoặc ghi số 5.

Lời giải:

Gọi A là biến cố: “Hai quả cầu lấy ra không có quả cầu nào ghi số 1”,

A₁ là biến cố: “Quả cầu lấy ra từ túi I không ghi số 1”,

A₂ là biến cố: “Quả cầu lấy ra từ túi II không ghi số 1”.

Ta có A = A₁A₂. Hai biến cố A₁ và A₂ độc lập nên P(A) = P(A₁) . P(A₂).

Lại có P(A₁) = P(A₂) = $\frac{9}{10}$ = 0,9. Do đó P(A) = (0,9)².

Gọi B là biến cố: “Hai quả cầu lấy ra không có quả cầu nào ghi số 5”,

B₁ là biến cố: “Quả cầu lấy ra từ túi I không ghi số 5”,

B₂ là biến cố: “Quả cầu lấy ra từ túi II không ghi số 5”.

Ta có B = B₁B₂. Hai biến cố B₁ và B₂ độc lập nên P(B) = P(B₁) . P(B₂).

Lại có P(B₁) = P(B₂) = $\frac{9}{10}$ = 0,9. Do đó P(B) = (0,9)².

Gọi E là biến cố: “Trong hai quả cầu lấy ra không có quả cầu nào ghi số 1 hoặc ghi số 5”.

Ta có E = A ∪ B.

Theo công thức cộng xác suất ta có P(E) = P(A) + P(B) – P(AB).

Ta có AB là biến cố: “Hai quả cầu lấy ra không có quả nào ghi số 1 và ghi số 5”.

Gọi H₁ là biến cố: “Quả cầu lấy ra từ túi I không ghi số 1 và số 5”,

H₂ là biến cố: “Quả cầu lấy ra từ túi II không ghi số 1 và số 5”.

Ta có AB = H₁H₂. Hai biến cố H₁ và H₂ độc lập nên P(AB) = P(H₁) . P(H₂).

Lại có P(H₁) = P(H₂) = $\frac{8}{10}$. Từ đó P(AB) = (0,8)².

Do đó, P(E) = P(A) + P(B) – P(AB) = (0,9)² + (0,9)² – (0,8)² = 0,98.

Vậy xác suất để trong hai quả cầu được lấy ra không có quả cầu nào ghi số 1 hoặc ghi số 5 là 0,98.

Bài 8.15 trang 78 Toán 11 Tập 2: Trong đợt kiểm tra cuối học kì II lớp 11 của các trường trung học phổ thông, thống kê cho thấy có 93% học sinh tỉnh X đạt yêu cầu; 87% học sinh tỉnh Y đạt yêu cầu. Chọn ngẫu nhiên một học sinh của tỉnh X và một học sinh của tỉnh Y. Giả thiết rằng chất lượng học tập của hai tỉnh là độc lập. Tính xác suất để:

a) Cả hai học sinh được chọn đều đạt yêu cầu;

b) Cả hai học sinh được chọn đều không đạt yêu cầu;

c) Chỉ có đúng một học sinh được chọn đạt yêu cầu;

d) Có ít nhất một trong hai học sinh được chọn đạt yêu cầu.

Lời giải:

Xác suất để học sinh tỉnh X không đạt yêu cầu là 100% – 93% = 7% = 0,07.

Xác suất để học sinh tỉnh Y không đạt yêu cầu là 100% – 87% = 13% = 0,13.

Gọi A là biến cố: “Học sinh tỉnh X đạt yêu cầu”.

B là biến cố: “Học sinh tỉnh Y đạt yêu cầu”.

Khi đó ta có P(A) = 0,93; P(B) = 0,87; P($\overline{A}$) = 0.07; P($\overline{B}$) = 0,13 .

a) Xác suất để cả hai học sinh được chọn đều đạt yêu cầu là:

P(AB) = P(A) . P(B) = 0,93 . 0,87 = 0,8091.

b) Xác suất để cả hai học sinh được chọn đều không đạt yêu cầu là:

P($\overline{A}$$\overline{B}$) = P($\overline{A}$).P($\overline{B}$) = 0,07 . 0,13 = 0,0091.

c) Xác suất để chỉ có đúng một học sinh được chọn đạt yêu cầu là:

P(A$\overline{B}$) + P($\overline{A}$B) = 0,93 . 0,13 + 0,07 . 0,87 = 0,1818.

d) Xác suất để có ít nhất một trong hai học sinh được chọn đạt yêu cầu là:

P(A ∪ B) = P(A) + P(B) – P(AB) = 0,93 + 0,87 – 0,8091 = 0,9909.

Xem thêm các bài giải SGK Toán 11 Kết nối tri thức hay, chi tiết khác: