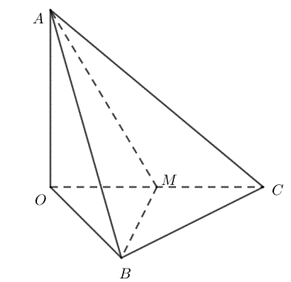
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = 2a, OB = 3a, OC = 8a. M là trung điểm đoạn OC. Tính thể tích V khối tứ diện OABM

44 04/05/2024

Cho tứ diện \(OABC\)có \(OA\), \(OB\), \(OC\) đôi một vuông góc với nhau và \(OA = 2a\), \(OB = 3a\), \(OC = 8a\). \(M\) là trung điểm đoạn \(OC\). Tính thể tích \(V\) khối tứ diện \(OABM\).

A. \(8{a^3}\).

B. \(3{a^3}\).

C. \(4{a^3}\).

D. \(6{a^3}\).

Trả lời

Lời giải

Chọn C

Media VietJack

Ta có: \(\left\{ {\begin{array}{*{20}{l}}{OA \bot OB}\\{OA \bot OC}\end{array}} \right. \Rightarrow OA \bot \left( {OBC} \right)\)

Thể tích khối tứ diện \(OABM\) là \(V = \frac{1}{3}.OA.{S_{\Delta OBM}} = \frac{1}{3}.OA.\frac{1}{2}.{S_{\Delta OBC}} = \frac{1}{6}.OA.\frac{1}{2}.OB.OC = \frac{1}{{12}}.2a.3a.8a = 4{a^3}\).

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

Câu hỏi cùng chủ đề

Cho hàm số y = f( x ). Hàm số y = f'( x )có đồ thị như hình bên. Hàm số g( x ) = f( x^2 + 2x) - x^2 - 2x đồng biến trên khoảng nào dưới đây? A. ( - 1 - căn bậc hai của 2 ; - 1).

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

79 6 tháng trước

Cho hàm số y = f( x ) có bảng biến thiên như sau Số nghiệm thuộc [ 0; 3pi /2] của phương trình | f( cos 2x)| = 1 là A. 9 B. 4 C. 7 D. 10

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

75 6 tháng trước

Cho hàm số y = f( x ) xác định, liên tục trên R và có đúng hai điểm cực trị x = - 1,x = 1, có đồ thị như hình vẽ sau: Hỏi hàm số y = f( x^2 - 2x + 1) + 2020 có bao nhiêu điểm cực tiểu?

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

91 6 tháng trước

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt đáy ( ABC), BC = a, góc hợp bởi (SBC) và ( ABC) là 60^0. Mặt phẳng ( P )qua A vuông góc với SC cắt SB,SC lần l

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

65 6 tháng trước

Số điểm cực trị của hàm số f( x ) có đạo hàm f'( x ) = ( x + 1)( x - 2)^2, x thuộc R là A. 0 B. 3 C. 1 D. 2

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

65 6 tháng trước

Đường cong ở hình vẽ dưới đây là đồ thị của hàm số y = ax + b/cx + d với (a,b,c,d) là các số thực. Mệnh đề nào dưới đây đúng ? A. y' < 0, x khác - 1. B. y' > 0, x thuộc R C. y' > 0, x

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

68 6 tháng trước

Cho hàm số y = căn bậc hai của x^2 - 2x - 3. Khẳng định nào sau đây là đúng? A. maxy = 1 B. maxy = 2 C. maxy = 0 D. Hàm số không có giá trị lớn nhất.

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

69 6 tháng trước

Cho hàm số bậc ba y = f( x ) có đồ thị như hình vẽ: Khi đó phương trình 2f( x) - 1 = 0 có bao nhiêu nghiệm thực phân biệt. A. 3. B. 0 C. 1. D. 2.

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

80 6 tháng trước

Tìm tất cả các giá trị thực của tham số m để hàm số y = - 1/3x^3 - mx^2 + ( 2m - 3)x + 2018 nghịch biến trên R A. - 3 nhỏ hơn bằng m nhỏ hơn bằng 1 B. - 3 < m < 1 C. m lớn hơn b

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

90 6 tháng trước

Biết đồ thị hàm số y = f( x ) có một tiệm cận ngang là y = 3. Khi đó đồ thị hàm số y = 2f( x ) - 4 có một tiệm cận ngang là A. y = 3 B. y = 2 C. y = 1 D. y = - 4

Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án

82 6 tháng trước

Xem tất cả

Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = 2a, OB = 3a, OC = 8a. M là trung điểm đoạn OC. Tính thể tích V khối tứ diện OABM

Trả lời

Câu hỏi cùng chủ đề

Cho hàm số y = f( x ). Hàm số y = f'( x )có đồ thị như hình bên. Hàm số g( x ) = f( x^2 + 2x) - x^2 - 2x đồng biến trên khoảng nào dưới đây? A. ( - 1 - căn bậc hai của 2 ; - 1).

Cho hàm số y = f( x ) có bảng biến thiên như sau Số nghiệm thuộc [ 0; 3pi /2] của phương trình | f( cos 2x)| = 1 là A. 9 B. 4 C. 7 D. 10

Cho hàm số y = f( x ) xác định, liên tục trên R và có đúng hai điểm cực trị x = - 1,x = 1, có đồ thị như hình vẽ sau: Hỏi hàm số y = f( x^2 - 2x + 1) + 2020 có bao nhiêu điểm cực tiểu?

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, SA vuông góc với mặt đáy ( ABC), BC = a, góc hợp bởi (SBC) và ( ABC) là 60^0. Mặt phẳng ( P )qua A vuông góc với SC cắt SB,SC lần l

Số điểm cực trị của hàm số f( x ) có đạo hàm f'( x ) = ( x + 1)( x - 2)^2, x thuộc R là A. 0 B. 3 C. 1 D. 2

Đường cong ở hình vẽ dưới đây là đồ thị của hàm số y = ax + b/cx + d với (a,b,c,d) là các số thực. Mệnh đề nào dưới đây đúng ? A. y' < 0, x khác - 1. B. y' > 0, x thuộc R C. y' > 0, x

Cho hàm số y = căn bậc hai của x^2 - 2x - 3. Khẳng định nào sau đây là đúng? A. maxy = 1 B. maxy = 2 C. maxy = 0 D. Hàm số không có giá trị lớn nhất.

Cho hàm số bậc ba y = f( x ) có đồ thị như hình vẽ: Khi đó phương trình 2f( x) - 1 = 0 có bao nhiêu nghiệm thực phân biệt. A. 3. B. 0 C. 1. D. 2.

Tìm tất cả các giá trị thực của tham số m để hàm số y = - 1/3x^3 - mx^2 + ( 2m - 3)x + 2018 nghịch biến trên R A. - 3 nhỏ hơn bằng m nhỏ hơn bằng 1 B. - 3 < m < 1 C. m lớn hơn b

Biết đồ thị hàm số y = f( x ) có một tiệm cận ngang là y = 3. Khi đó đồ thị hàm số y = 2f( x ) - 4 có một tiệm cận ngang là A. y = 3 B. y = 2 C. y = 1 D. y = - 4

Danh mục