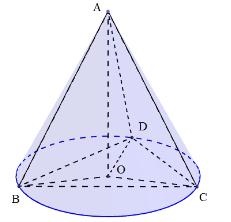
Cho tứ diện đều ABC có cạnh 3a. Hình nón \(\left( N \right)\) có đỉnh A và đường tròn đáy là đường tròn ngoại tiếp tam giác BCD. Tính diện tích xung quanh của hình nón \(\left( N \right)\)

D. \[6\sqrt 3 \pi {a^2}\]

Đáp án B

Phương pháp:

Diện tích xung quanh của hình nón \({S_{xq}} = \pi rl\)

Cách giải:

Gọi O là tâm của tam giác BCD \( \Rightarrow AO \bot \left( {BCD} \right)\)

\(OD = \frac{2}{3}.\frac{{3a\sqrt 3 }}{2} = a\sqrt 3 \)

Diện tích xung quanh của hình nón \({S_{xq}} = \pi .OD.AD = \pi .a\sqrt 3 .3a = 3\sqrt 3 \pi {a^2}\)