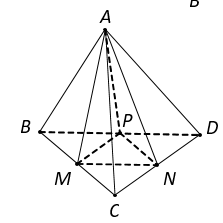
Cho tứ diện ABCD có các cạnh AB,AC và AD đôi một vuông góc với nhau; $AB=6a,AC=7a$  và $AD=4a.$  Gọi $M,N,P$  tương ứng là trung điểm các cạnh $BC,CD,BD.$  Tính thể tích V của tứ diện  AMNP

A. $V=\frac{7}{2}{a}^3.$

Do $AB,AC$  và AD đôi một vuông góc với nhau nên

$V_{ABCD}=\frac{1}{6}AB.AC.AD=\frac{1}{6}.6a.7a.4a=28a^3.$

Dễ thấy $S_{\Delta MNP}=\frac{1}{4}{S}_{\Delta BCD}$ .

Suy ra $V_{AMNP}=\frac{1}{4}{V}_{ABCD}=7a^3$ . Chọn D.