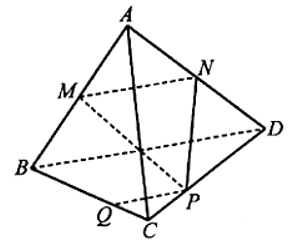
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD và P là một điểm nằm trên CD
Bài 16 trang 100 SBT Toán 11: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, AD và P là một điểm nằm trên CD. Đường thẳng BC cắt mặt phẳng (MNP) tại Q. Chứng minh rằng PQ // BD.