Bài 6 trang 100 Toán 11 Tập 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA; I, J, K, L lần lượt là trung điểm của các đoạn thẳng SM, SN, SP, SQ.
a) Chứng minh rằng bốn điểm I, J, K, L đồng phẳng và tứ giác IJKL là hình bình hành.
b) Chứng minh rằng IK // BC.
c) Xác định giao tuyến của hai mặt phẳng (IJKL) và (SBC).
a)
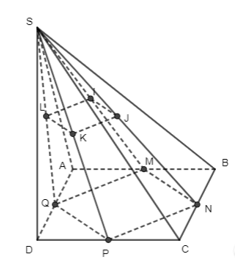
Trong tam giác SMN, có: IJ // MN (tính chất đường trung bình) và IJ = MN.
Trong tam giác SQP, có: LK // QP (tính chất đường trung bình) và LK = PQ.
Mà QP // AC // MN (tính chất đường trung bình) và PQ = MN = AC
Do đó IJ // LK và IJ = LK
Vậy qua hai đường thẳng song song ta xác định được duy nhất một mặt phẳng chứa hai đường thẳng song song đó hay I, J, K, L đồng phẳng.
Xét tứ giác IJKL có IJ // LK và IJ = LK nên IJKL là hình bình hành.
b)
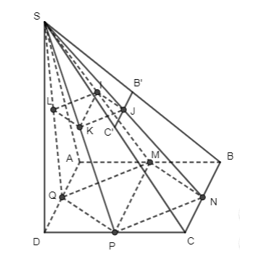
Trong tam giác SMP có: IK // MP (tính chất đường trung bình tam giác SMP)
Mà MP // AD // BC (tính chất đường trung bình của hình thang)
Suy ra IK // BC.
c) Ta có: J ∈ SN mà SN ⊂ (SBC) nên J ∈ (SBC)
Lại có J ∈ (IJKL)
Do đó J là giao điểm của (IJKL) và (SBC).
Mặt khác: IK // BC (chứng minh trên);
IK ⊂ (IJKL);
BC ⊂ (SBC).
Do đó giao tuyến của hai mặt phẳng (IJKL) và (SBC) là đường thẳng đi qua J song song với BC cắt SB, SC lần lượt tại B’ và C’.
Vậy (IJKL) ∩ (SBC) = B’C’.
Xem thêm các bài giải SGK Toán lớp 11 Cánh diều hay, chi tiết khác:
Bài 1: Đường thẳng và mặt phẳng trong không gian
Bài 2: Hai đường thẳng song song trong không gian
Bài 3: Đường thẳng và mặt phẳng song song