Cho tứ diện ABCD, có \(AB = AC = AD = a,\,\,\,BAD = {90^0};\,\,DAC = {60^0};\,\,CAB = {120^0}\). Thể tích tứ diện ABCD là
D. \(\frac{{{a^3}\sqrt 3 }}{{12}}\)
Đáp án B
Phương pháp:
+) Chóp có các cạnh bên bằng nhau thì chân đường cao trùng với tâm đường tròn ngoại tiếp đáy.
+) Tính độ dài các cạnh BC, CD, DA, sử dụng định lí Pytago đảo chứng minh tam giác ABC vuông.
+)
Cách giải:
Tam giác ABD vuông cân tại A \( \Rightarrow BD = AB\sqrt 2 = a\sqrt 2 \)
Tam giác ACD đều \( \Rightarrow CD = AD = a\)
Tam giác ABC: \(BC = \sqrt {A{B^2} + A{C^2} - 2.AB.AC.\cos {{120}^0}} = \sqrt {{a^2} + {a^2} - 2.{a^2}.\frac{{ - 1}}{2}} = a\sqrt 3 \)
\( \Rightarrow B{D^2} + C{D^2} = B{C^2} \Rightarrow \) Tam giác BCD vuông tại D
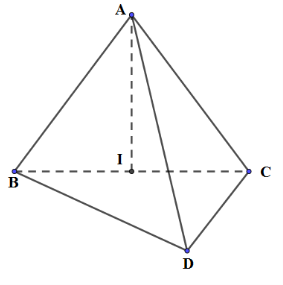
Gọi I là trung điểm của BC \( \Rightarrow \) I là tâm đường tròn ngoại tiếp tam giác BCD
Mà tứ diện ABCD có \(AB = AC = AD\)
\( \Rightarrow AI \bot \left( {BCD} \right) \Rightarrow {V_{ABCD}} = \frac{1}{3}.AI.{S_{BCD}}\)
Tam giác ABI vuông tại I \( \Rightarrow AI = \sqrt {A{B^2} - B{I^2}} = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}} = \frac{a}{2}\)
Tam giác BCD vuông tại D \( \Rightarrow {S_{BCD}} = \frac{1}{2}.BD.DC = \frac{1}{2}.a\sqrt 2 .a = \frac{{{a^2}\sqrt 2 }}{2}\)
\( \Rightarrow {V_{ABCD}} = \frac{1}{3}.AI.{S_{BCD}} = \frac{1}{3}.\frac{a}{2}.\frac{{{a^2}\sqrt 2 }}{2} = \frac{{{a^3}\sqrt 2 }}{{12}}\)
Tam giác ABD vuông cân tại A \( \Rightarrow BD = AB\sqrt 2 = a\sqrt 2 \)
Tam giác ACD đều \( \Rightarrow CD = AD = a\)
Tam giác ABD vuông cân tại A \( \Rightarrow BD = AB\sqrt 2 = a\sqrt 2 \)
Tam giác ACD đều \( \Rightarrow CD = AD = a\)
Tam giác ABC: \(BC = \sqrt {A{B^2} + A{C^2} - 2.AB.AC.\cos {{120}^0}} = \sqrt {{a^2} + {a^2} - 2.{a^2}.\frac{{ - 1}}{2}} = a\sqrt 3 \)
\( \Rightarrow B{D^2} + C{D^2} = B{C^2} \Rightarrow \) Tam giác BCD vuông tại D
Gọi I là trung điểm của BC \( \Rightarrow \) I là tâm đường tròn ngoại tiếp tam giác BCD
Mà tứ diện ABCD có \(AB = AC = AD\)
\( \Rightarrow AI \bot \left( {BCD} \right) \Rightarrow {V_{ABCD}} = \frac{1}{3}.AI.{S_{BCD}}\)
Tam giác ABI vuông tại I \( \Rightarrow AI = \sqrt {A{B^2} - B{I^2}} = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}} = \frac{a}{2}\)
Tam giác BCD vuông tại D \( \Rightarrow {S_{BCD}} = \frac{1}{2}.BD.DC = \frac{1}{2}.a\sqrt 2 .a = \frac{{{a^2}\sqrt 2 }}{2}\)
\( \Rightarrow {V_{ABCD}} = \frac{1}{3}.AI.{S_{BCD}} = \frac{1}{3}.\frac{a}{2}.\frac{{{a^2}\sqrt 2 }}{2} = \frac{{{a^3}\sqrt 2 }}{{12}}\)
Tam giác ABC: \(BC = \sqrt {A{B^2} + A{C^2} - 2.AB.AC.\cos {{120}^0}} = \sqrt {{a^2} + {a^2} - 2.{a^2}.\frac{{ - 1}}{2}} = a\sqrt 3 \)
\( \Rightarrow B{D^2} + C{D^2} = B{C^2} \Rightarrow \) Tam giác BCD vuông tại D
Gọi I là trung điểm của BC \( \Rightarrow \) I là tâm đường tròn ngoại tiếp tam giác BCD
Mà tứ diện ABCD có \(AB = AC = AD\)
\( \Rightarrow AI \bot \left( {BCD} \right) \Rightarrow {V_{ABCD}} = \frac{1}{3}.AI.{S_{BCD}}\)
Tam giác ABI vuông tại I \( \Rightarrow AI = \sqrt {A{B^2} - B{I^2}} = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}} = \frac{a}{2}\)
Tam giác BCD vuông tại D \( \Rightarrow {S_{BCD}} = \frac{1}{2}.BD.DC = \frac{1}{2}.a\sqrt 2 .a = \frac{{{a^2}\sqrt 2 }}{2}\)
\( \Rightarrow {V_{ABCD}} = \frac{1}{3}.AI.{S_{BCD}} = \frac{1}{3}.\frac{a}{2}.\frac{{{a^2}\sqrt 2 }}{2} = \frac{{{a^3}\sqrt 2 }}{{12}}\)