Luyện tập 2 trang 105 Toán 7 Tập 2: Cho tam giác PQR có hai đường trung tuyến QM và RK cắt nhau tại G. Gọi I là trung điểm của cạnh QR. Chứng minh rằng ba điểm P, G, I thẳng hàng.
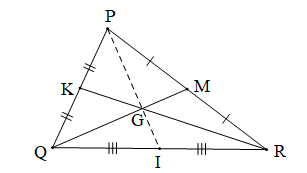
Tam giác PQR có hai đường trung tuyến QM và RK cắt nhau tại G (giả thiết) nên G là trọng tâm của tam giác PQR.
I là trung điểm của cạnh QR nên PI là đường trung tuyến của tam giác PQR kẻ từ đỉnh P.
Mà các đường trung tuyến của tam giác cùng đi qua trọng tâm của tam giác nên trung tuyến PI sẽ đi qua điểm G.
Vậy ba điểm P, G, I thẳng hàng.
Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 8: Đường vuông góc và đường xiên
Bài 9: Đường trung trực của một đoạn thẳng
Bài 10: Tính chất ba đường trung tuyến của tam giác
Bài 11: Tính chất ba đường phân giác của tam giác