Cho tam giác ABC. Ba đường trung tuyến AM, BN, CP đồng quy tại G. Chứng minh: GA + GB + GC = 2/3.(AM + BN + CP)

Bài 1 trang 107 Toán 7 Tập 2: Cho tam giác ABC. Ba đường trung tuyến AM, BN, CP đồng quy tại G. Chứng minh:

GA + GB + GC = $\frac{2}{3}$(AM + BN + CP).

Trả lời

Chứng minh (Hình vẽ dưới đây):

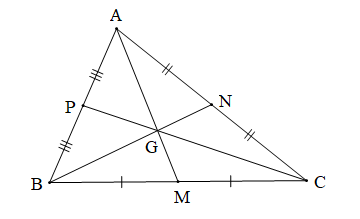
Tam giác ABC có ba đường trung tuyến AM, BN, CP đồng quy tại G nên G là trọng tâm của tam giác ABC.

Khi đó AG = $\frac{2}{3}$AM; BG = $\frac{2}{3}$BN; CG = $\frac{2}{3}$CP (tính chất trọng tâm của tam giác)

Do đó GA + GB + GC = $\frac{2}{3}$AM + $\frac{2}{3}$BN + $\frac{2}{3}$CP = $\frac{2}{3}$(AM + BN + CP).

Vậy GA + GB + GC = $\frac{2}{3}$(AM + BN + CP).

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

Bài 8: Đường vuông góc và đường xiên

Bài 9: Đường trung trực của một đoạn thẳng

Bài 10: Tính chất ba đường trung tuyến của tam giác

Bài 11: Tính chất ba đường phân giác của tam giác

Bài 12: Tính chất ba đường trung trực của tam giác

Bài 13: Tính chất ba đường cao của tam giác