Cho tam giác nhọn ABC. Hai đường cao BE và CF cắt nhau tại H, góc HCA = 25°. Tính góc BAC và góc HBA
Bài 4 trang 118 Toán 7 Tập 2: Cho tam giác nhọn ABC. Hai đường cao BE và CF cắt nhau tại H, . Tính và .
Bài 4 trang 118 Toán 7 Tập 2: Cho tam giác nhọn ABC. Hai đường cao BE và CF cắt nhau tại H, . Tính và .
|
GT |
DABC nhọn, BE AC, CF AB, BE và CF cắt nhau tại H, |
|
KL |
Tính và . |
Chứng minh (Hình vẽ dưới đây):
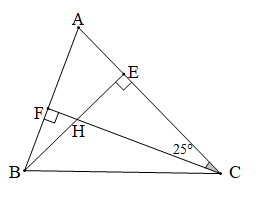
Vì CF AB (giả thiết) nên tam giác ACF vuông tại F.
Xét ACF vuông tại F: (trong tam giác vuông, hai góc nhọn phụ nhau).
Suy ra hay .
Vì BE AC (giả thiết) nên tam giác ABE vuông tại E.
Xét ABE vuông tại E: (trong tam giác vuông, hai góc nhọn phụ nhau).
Suy ra hay .
Vậy và .
Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 10: Tính chất ba đường trung tuyến của tam giác
Bài 11: Tính chất ba đường phân giác của tam giác
Bài 12: Tính chất ba đường trung trực của tam giác