Cho tam giác đều có cạnh bằng a, gọi là tam giác H1. Nỗi các trung điểm của H1 để tạo thành tam giác H2. Tiếp theo, nối các trung điểm của H2

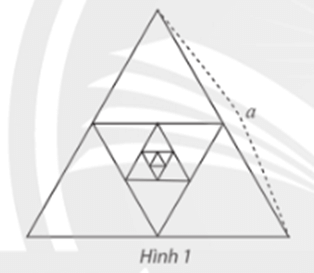
Bài 7 trang 86 Toán 11 Tập 1: Cho tam giác đều có cạnh bằng a, gọi là tam giác H₁. Nỗi các trung điểm của H₁ để tạo thành tam giác H₂. Tiếp theo, nối các trung điểm của H₂ để tạo thành tam giác H₃ (Hình 1). Cứ tiếp tục như vậy, nhận được dãy tam giác H₁, H₂, H₃, ...

Tỉnh tổng chu vi và tổng diện tích của các tam giác của dãy.

Trả lời

Ta có:

Diện tích tam giác H₁ = S và chu vi tam giác H₁ = 3a;

Diện tích tam giác H₂ = $\frac{1}{4}$S và chu vi tam giác H₂ = $\frac{1}{2}$3a;

Diện tích tam giác H₂ = ${\left(\frac{1}{4}\right)}^2$S và chu vi tam giác H₃ = ${\left(\frac{1}{2}\right)}^2$3a;

...

Diện tích tam giác H_n = ${\left(\frac{1}{4}\right)}^{n-1}$S và chu vi tam giác H₂ = ${\left(\frac{1}{2}\right)}^{n-1}$3a;

Khi đó:

Diện tích của dãy các tam giác H₁; H₂; H₃; ...; H₄ lập thành một cấp số nhân lùi vô hạn có số hạng đầu tiên u₁ = S và công bội q = $\frac{1}{4}$ có tổng bằng $S+\frac{1}{4}S+{\left(\frac{1}{4}\right)}^{2}S+\mathrm{...}+{\left(\frac{1}{4}\right)}^{n-1}S+\mathrm{...}=\frac{S}{1-\frac{1}{4}}=\frac{4}{3}S$.

Diện tích của dãy các tam giác H₁; H₂; H₃; ...; H₄ lập thành một cấp số nhân lùi vô hạn có số hạng đầu tiên u₁ = 3a và công bội q = $\frac{1}{2}$ có tổng bằng

$3a+\frac{1}{2}.3a+{\left(\frac{1}{2}\right)}^2.3a+{\left(\frac{1}{2}\right)}^3.3a+\mathrm{...}+{\left(\frac{1}{2}\right)}^{n-1}3a+\mathrm{...}=\frac{3a}{1-\frac{1}{2}}=6a$.

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Giới hạn của hàm số

Bài 3: Hàm số liên tục

Bài tập cuối chương 3

Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian

Bài 2: Hai đường thẳng song song

Bài 3: Đường thẳng và mặt phẳng song song