Cho tam giác ABC vuông tại A có đường cao AH Chứng minh A là trung điểm của DE
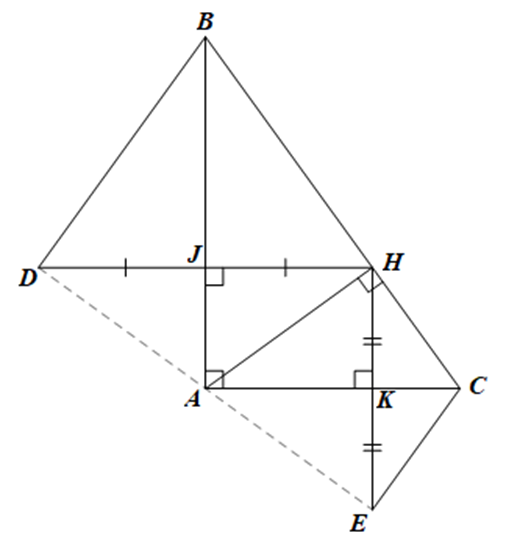
Cho tam giác ABC vuông tại A có đường cao AH. Kẻ HJ vuông góc với AB tại J và HK vuông góc với AC tại K. Trên tia HJ lấy điểm D sao cho DJ = JH. Trên tia HK lấy điểm E sao cho EK = KH.
Chứng minh A là trung điểm của DE.