Cho tam giác ABC và M là trung điểm của đoạn thẳng BC. Giả sử AM vuông góc với BC
984
22/10/2023
Bài 4.25 trang 84 Toán 7 Tập 1: Cho tam giác ABC và M là trung điểm của đoạn thẳng BC.
a) Giả sử AM vuông góc với BC. Chứng minh rằng tam giác ABC cân tại A.
b) Giả sử AM là tia phân giác của góc BAC. Chứng minh rằng tam giác ABC cân tại A.
Trả lời
a)
|
GT
|
, M là trung điểm BC, .
|
|
KL
|
cân tại A.
|
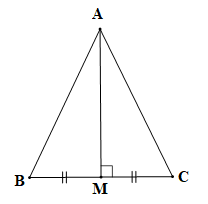
Vì M là trung điểm của BC và (theo giả thiết) nên đường thẳng AM là đường trung trực của đoạn thẳng BC.
Điểm A nằm trên đường trung trực của đoạn thẳng BC nên AB = AC (tính chất đường trung trực của một đoạn thẳng).
Do đó tam giác ABC cân tại A (định nghĩa tam giác cân).
b)
|
GT
|
, M là trung điểm BC;
AM là tia phân giác của góc BAC.
|
|
KL
|
cân tại A.
|
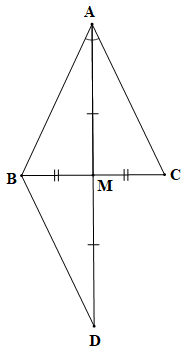
Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
Xét tam giác DBM và tam giác ACM có:
BM = CM (do M là trung điểm của BC);
(hai góc đối đỉnh);
MD = MA (theo cách vẽ).
Vậy (c.g.c).
Suy ra DB = AC (hai cạnh tương ứng) . (1)
Và (hai góc tướng ứng).
Mà (do AM là tia phân giác của góc BAC).
Do đó .
Hay suy ra tam giác ABD cân tại B.
Suy ra AB = DB (định nghĩa tam giác cân). (2)
Từ (1) và (2) suy ra AB = AC.
Do đó tam giác ABC cân tại A (định nghĩa tam giác cân).
Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:
Luyện tập chung trang 74
Bài 15: Các trường hợp bằng nhau của tam giác vuông
Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng
Luyện tập chung trang 86
Bài tập cuối chương 4 trang 87
Bài 17: Thu thập và phân loại dữ liệu


