Cho tam giác ABC. Trên cạnh BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho CE = BD. Gọi O là giao điểm của DE và BC

Bài 51* trang 84 SBT Toán 7 Tập 2: Cho tam giác ABC. Trên cạnh BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho CE = BD. Gọi O là giao điểm của DE và BC. Biết OD = OE. Chứng minh tam giác ABC là tam giác cân.

Trả lời

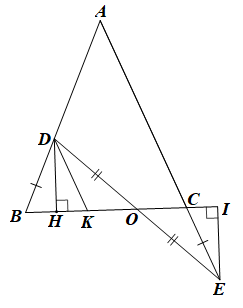
Qua D vẽ DK // AC (K ∈ BC) nên $\widehat{KDO}=\widehat{OEC}$ (hai góc so le trong).

Xét $∆$OKD và $∆$OCE có:

$\widehat{KDO}=\widehat{OEC}$ (chứng minh trên),

OD = OE (giả thiết),

$\widehat{DOK}=\widehat{EOC}$ (hai góc đối đỉnh).

Do đó ∆OKD = ∆OCE (g.c.g).

Suy ra KD = CE (hai cạnh tương ứng).

Mặt khác BD = CE suy ra DB = DK hay tam giác DBK cân tại D.

Suy ra $\widehat{DBK}=\widehat{DKB}$ (1)

Do DK // AC nên $\widehat{DKB}=\widehat{ACB}$ (hai góc đồng vị) (2)

Từ (1) và (2) ta có: $\widehat{ABC}=\widehat{ACB}$.

Suy ra tam giác ABC cân tại A.

Vậy tam giác ABC là tam giác cân tại A.

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh

Bài 6. Trường hợp bằng nhau thứ ba của tam giác:

Bài 7. Tam giác cân

Bài 8. Đường vuông góc và đường xiên

Bài 9. Đường trung trực của một đoạn thẳng

Bài 10. Tính chất ba đường trung tuyến của tam giác