Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh vectơ PB + vectơ MC = vectơ AN

Luyện tập 1 trang 84 Toán lớp 10 Tập 1: Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh $\overrightarrow{PB}+\overrightarrow{MC}=\overrightarrow{AN}$.

Trả lời

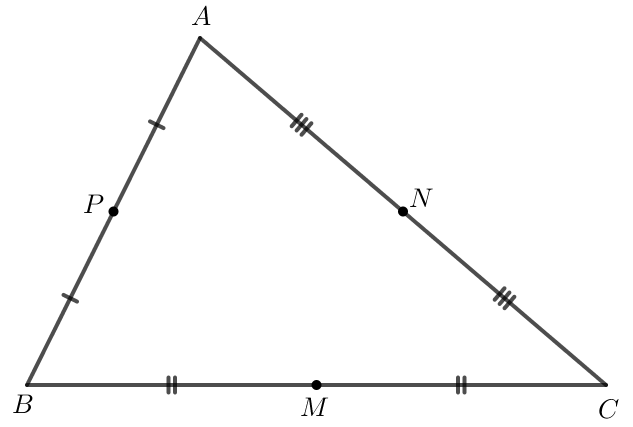
Do P là trung điểm của AB nên $\overrightarrow{AP}=\overrightarrow{PB}$.

Do đó $\overrightarrow{AP}+\overrightarrow{PB}=\overrightarrow{PB}+\overrightarrow{PB}$ hay $\overrightarrow{AB}=\overrightarrow{PB}+\overrightarrow{PB}$.

Do M là trung điểm của BC nên $\overrightarrow{MC}=\overrightarrow{BM}$.

Do đó $\overrightarrow{BM}+\overrightarrow{MC}=\overrightarrow{BM}+\overrightarrow{BM}$ hay $\overrightarrow{BC}=\overrightarrow{BM}+\overrightarrow{BM}$.

Do N là trung điểm của AC nên $\overrightarrow{AN}=\overrightarrow{NC}$.

Do đó $\overrightarrow{AN}+\overrightarrow{NC}=\overrightarrow{NC}+\overrightarrow{NC}$ hay $\overrightarrow{AC}=\overrightarrow{NC}+\overrightarrow{NC}$.

Mà $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$ hay $\overrightarrow{PB}+\overrightarrow{PB}+\overrightarrow{MC}+\overrightarrow{MC}=\overrightarrow{NC}+\overrightarrow{NC}$.

Do đó $\overrightarrow{PB}+\overrightarrow{MC}=\overrightarrow{AN}$.

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh Diều hay, chi tiết khác:

Bài 2: Giải tam giác. Tính diện tích tam giác

Bài 3: Khái niệm vectơ

Bài 4: Tổng và hiệu của hai vectơ

Bài 5: Tích của một số với một vectơ

Bài 6: Tích vô hướng của hai vectơ

Bài tập cuối chương 4