Cho tam giác ABC có G là trọng tâm. Đường thẳng qua G song song với BC lần lượt cắt cạnh AB, AC tại M, N. Chứng minh AM/AB = AN/AC = 2/3

Luyện tập 2 trang 53 Toán 8 Tập 2: Cho tam giác ABC có G là trọng tâm. Đường thẳng qua G song song với BC lần lượt cắt cạnh AB, AC tại M, N. Chứng minh $\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}=\frac{2}{3}.$

Trả lời

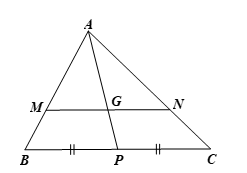
Gọi P là trung điểm của BC.

Xét ∆ABP với MG // BN (do G ∈ MN, P ∈ BC), ta có:

$\frac{\mathrm{AM}}{\mathrm{MB}}=\frac{\mathrm{AG}}{\mathrm{GP}}$ (định lí Thalès)

Suy ra $\frac{\mathrm{AM}}{\mathrm{AG}}=\frac{\mathrm{MB}}{\mathrm{GP}}$ (tính chất tỉ lệ thức)

Do đó $\frac{\mathrm{AM}}{\mathrm{AG}}=\frac{\mathrm{MB}}{\mathrm{GP}}=\frac{\mathrm{AM}+\mathrm{MB}}{\mathrm{AG}+\mathrm{GP}}=\frac{\mathrm{AB}}{\mathrm{AP}}$ (tính chất dãy tỉ số bằng nhau)

Hay $\frac{\mathrm{AM}}{\mathrm{AG}}=\frac{\mathrm{AB}}{\mathrm{AP}},$ nên $\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AG}}{\mathrm{AP}}.$

Mà G là trọng tâm ∆ABC nên $\frac{\mathrm{AG}}{\mathrm{AP}}=\frac{2}{3}$ (tính chất trọng tâm của một tam giác)

Do đó, $\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AG}}{\mathrm{AP}}=\frac{2}{3}$ (1)

Tương tự, xét ∆ABC với MN // BC ta cũng có $\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}$ (2)

Từ (1) và (2), suy ra $\frac{\mathrm{AM}}{\mathrm{AB}}=\frac{\mathrm{AN}}{\mathrm{AC}}=\frac{2}{3}.$

Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác: