Cho hình thang ABCD (AB // CD) có AB = 4 cm, CD = 6 cm. Đường thẳng d song song với hai đáy
1.5k
04/12/2023
Bài 2 trang 57 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD) có AB = 4 cm, CD = 6 cm. Đường thẳng d song song với hai đáy và cắt hai cạnh bên AD, BC của hình thang đó lần lượt tại M, N; cắt đường chéo AC tại P.
a) Chứng minh AMMD=BNNC;
b) Tính độ dài các đoạn thẳng MP, PN, MN; biết rằng MD = 2MA.
Trả lời
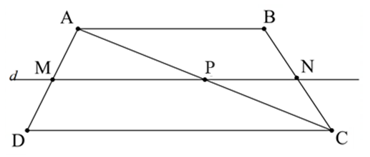
a) Do d // CD, mà M, N, P ∈ d nên MP // CD, PN // CD, MN // CD
Do ABCD là hình thang nên AB // CD, do đó PN // AB
Xét ∆ADC với MP // CD, ta có AMMD=APPC (định lí Thalès) (1)
Xét ∆ABC với PN // AB, ta có APPC=BNNC (định lí Thalès) (2)
Từ (1) và (2) suy ra AMMD=BNNC (=APPC).
b) ⦁Do MD = 2MA nên MAMD=12.
Suy ra MAMD+MA=12+1 hay AMAD=13.
⦁Xét ∆ADC với MP // CD, ta có AMAD=APAC=MPDC (hệ quả định lí Thalès)
Suy ra MPDC=APAC=AMAD=13. Do đó MP=DC3=63=2(cm).
⦁ Tương tự, xét ∆ABC vớiPN // AB, ta có CNBC=CPAC=PNAB (hệ quả định lí Thalès)
Mà APAC=13 hay AC−CPAC=13, do đó 1−CPAC=13 nên CPAC=1−13=23.
Khi đó PNAB=CPAC=23 nên PN=23AB=23⋅4=83(cm).
Ta có: MN=MP+PN=2+83=143(cm).
Xem thêm các bài giải SGK Toán lớp 8 Cánh Diều hay, chi tiết khác:

