Cho tam giác ABC có AM là đường trung tuyến (M ∈ BC). Lấy điểm E thuộc AM sao cho AE = 3EM. Tia BE cắt AC tại N

Bài 5 trang 42 sách bài tập Toán 8 Tập 2: Cho tam giác ABC có AM là đường trung tuyến (M ∈ BC). Lấy điểm E thuộc AM sao cho AE = 3EM. Tia BE cắt AC tại N.

Tính tỉ số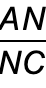 

Trả lời

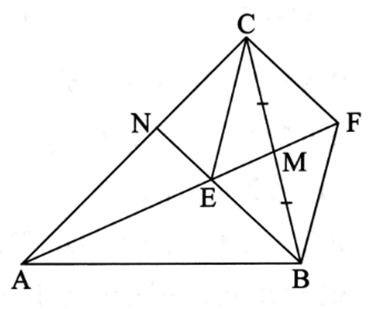
Lấy điểm F trên tia AM sao cho M là trung điểm của EF.

Tứ giác MEFC có hai hai đường chéo BC và EF cắt nhau tại trung điểm của mỗi đường nên tứ giác MEFC là hình bình hành.

Suy ra CF // BE và CF // EN.

Ta có AE = 3EM và ME = MF (vì M là trung điểm của EF).

Khi đó, $\frac{AE}{EF}=\frac{3}{2}$.

Xét ∆ACF có CF // EN nên theo định lí Thalès, ta có: $\frac{AN}{NC}=\frac{AE}{EF}=\frac{3}{2}$.

Vậy $\frac{AN}{NC}=\frac{3}{2}$.

Xem thêm các bài giải sách bài tập Toán 8 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Giải bài toán bằng cách lập phương trình bậc nhất

Bài tập cuối chương 6

Bài 1: Định lí Thalès trong tam giác

Bài 2: Đường trung bình của tam giác

Bài 3: Tính chất đường phân giác của tam giác

Bài tập cuối chương 7