Cho số phức z thỏa mãn trị tuyệt đối z + i = trị tuyệt đối z ngang + 2 + i. Giá trị nhỏ nhất của P = trị tuyệt đối (i - 1)z + 4 - 2i là
Cho z số phức thỏa mãn . Giá trị nhỏ nhất của là
A. 1
B.
C. 3
D.
A. 1
B.
C. 3
D.
Chọn C
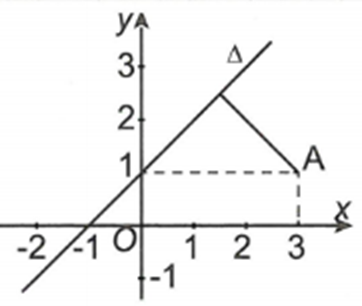
Gọi là điểm biểu diễn số phức z
Ta có
Ta có
, với
Đẳng thức xảy ra khi M là hình chiếu vuông góc của A trên đường thẳng hay