Cho S.ABCD là hình chóp tứ giác đều, biết AB = a, SA = a. Thể tích của khối chóp S.ABCD bằng A. a^3 căn bậc hai của 2 /2 B. a^3/3 C. a^3 căn bậc hai của 2 /6 D. a^3
64
25/04/2024
Cho S.ABCDlà hình chóp tứ giác đều, biết AB=a,SA=a. Thể tích của khối chóp S.ABCD bằng
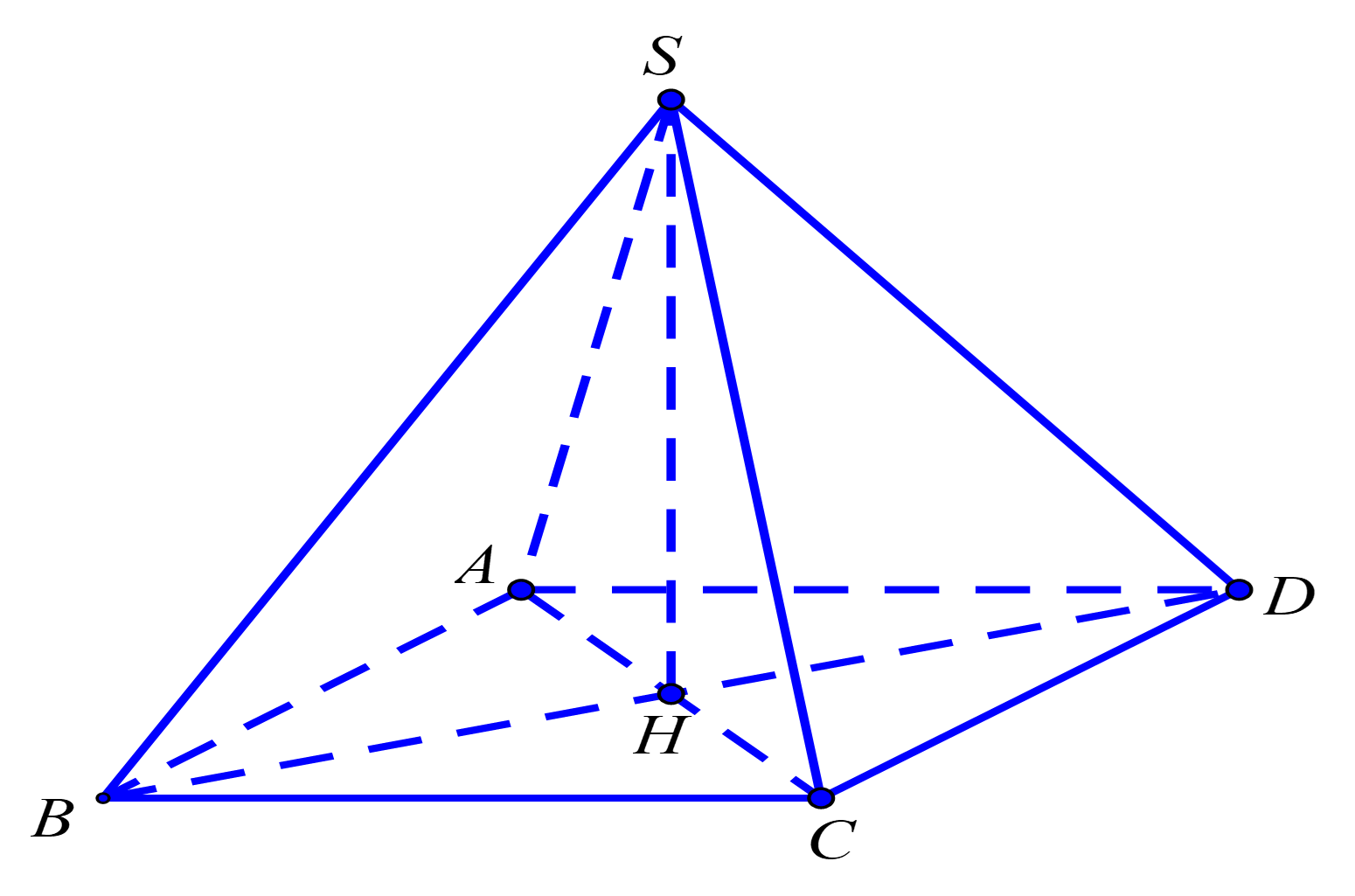
A. a3√22.
B. a33.
C. a3√26.
D. a3.
Trả lời
Lời giải
Chọn C
Gọi H là giao của AC và BD.
Vì S.ABCDlà hình chóp tứ giác đều nên SH⊥(ABCD).
Ta có: AC=√AD2+DC2=√a2+a2=a√2⇒AH=a√22.
Tam giác SHA vuông tại H nên có: SH=√SA2−AH2=√a2−(a√22)2=a√22.
Diện tích hình vuông ABCD là: SABCD=a2.
Thể tích của khối chóp S.ABCDlà: VS.ABCD=13SABCD.SH=13a2.a√22=a3√26.

