Cho P(x) = x^3 + x^2 + x + 1 và Q(x) = x^4 - 1. Tìm đa thức A(x) sao cho
Bài 9 trang 69 Toán 7 Tập 2:
Cho P(x) = x3 + x2 + x + 1 và Q(x) = x4 - 1. Tìm đa thức A(x) sao cho P(x).A(x) = Q(x).
Bài 9 trang 69 Toán 7 Tập 2:
Cho P(x) = x3 + x2 + x + 1 và Q(x) = x4 - 1. Tìm đa thức A(x) sao cho P(x).A(x) = Q(x).
Ta có: P(x).A(x) = Q(x)
Suy ra A(x) = Q(x) : P(x).
Thực hiện phép chia đa thức ta được:
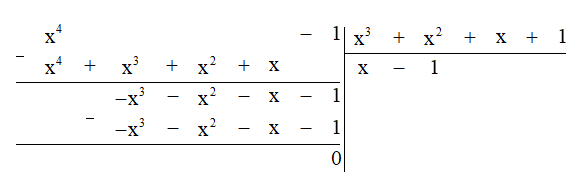
Do đó Q(x) : P(x) = x – 1
Vậy A(x) = x - 1.
Xem thêm lời giải SGK Toán lớp 7 Cánh diều hay, chi tiết khác:
Bài 4: Phép nhân đa thức một biến
Bài 5: Phép chia đa thức một biến
Bài 1: Tổng các góc của một tam giác
Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác