Cho mặt nón có chiều cao h = 6, bán kính đáy r = 3. Hình lập phương ABCD.A'B'C'D' đặt trong
45
26/04/2024
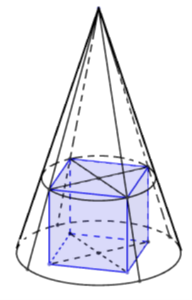
Cho mặt nón có chiều cao \(h = 6\), bán kính đáy \(r = 3\). Hình lập phương ABCD.A’B’C’D’ đặt trong mặt nón sao cho trục của mặt nón đi qua tâm hai đáy của hình lập phương, một đáy của hình lập phương nằm trong cùng một mặt phẳng đáy của hình trụ, các đỉnh của đáy còn lại thuộc các đường sinh của hình nón. Độ dài đường chéo của hình lập phương bằng
A. \(3\sqrt 3 \)
B. \(\frac{{3\sqrt 6 }}{2}\)
C. \(6\sqrt 3 \left( {\sqrt 2 - 1} \right)\)
D. \(6\left( {\sqrt 2 - 1} \right)\)
Trả lời
Đáp án A
Phương pháp:
Cắt khối hình bởi mặt phẳng đi qua trục
Tính độ dài x cạnh của hình lập phương
Tính độ dài đường chéo của hình lập phương: \(x\sqrt 3 \)
Cách giải:
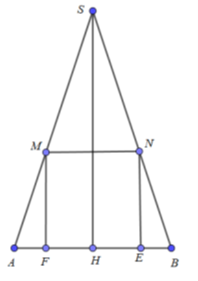
Xét mặt cắt qua trục có \(SH = h = 6,\,\,\,HA = HB = r = 3\)
Gọi độ dài cạnh của hình vuông là x.
Vì MN // AB nên \(\frac{{MN}}{{AB}} = \frac{{SN}}{{SB}} \Leftrightarrow \frac{x}{{2.3}} = \frac{{SN}}{{SB}} = \frac{x}{6}\)
Vì NE // SH nên \(\frac{{NE}}{{SH}} = \frac{{NB}}{{SB}} \Leftrightarrow \frac{x}{6} = \frac{{NE}}{{SB}}\)
\( \Rightarrow \frac{x}{6} + \frac{x}{6} = \frac{{SN}}{{SB}} + \frac{{NE}}{{SB}} = 1 \Rightarrow X = 3\)
\( \Rightarrow \) Độ dài đường chéo của hình lập phương là: \(3\sqrt 3 \)